Một phân xưởng có hai máy đặc chủng \({M_1}\), \({M_2}\) sản xuất hai loại sản phẩm kí hiệu là A và B. Một tấn sản phẩm loại A lãi 2 triệu đồng, một tấn sản phẩm loại B lãi 1,6 triệu đồng. Muốn sản xuất một tấn sản phẩm loại A phải dùng máy \({M_1}\) trong 3 giờ và máy \({M_2}\) trong 1 giờ. Muốn sản xuất một tấn sản phẩm loại B phải dùng máy
\({M_1}\) trong 1 giờ và máy \({M_2}\) trong 1 giờ. Một máy không thể dùng để sản xuất đồng thời hai loại sản phẩm. Máy \({M_1}\) làm việc không quá 6 giờ một ngày, máy \({M_2}\) làm việc không quá 4 giờ một ngày. Hỏi số tiền lãi lớn nhất mà phân xưởng này có thể thu được trong một ngày là bao nhiêu (đơn vị: triệu đồng)?
Đáp án:
Đáp án:
Lập hệ bất phương trình.
Gọi x, y lần lượt là số tấn sản phẩm loại A, B mà phân xưởng này sản xuất trong một ngày (\(x,y \ge 0\)).
Số giờ làm việc trong ngày của máy \({M_1}\) là 3x + y (giờ), số giờ làm việc trong ngày của máy \({M_1}\) là x + y (giờ).
Vì mỗi ngày, máy \({M_1}\) làm việc không quá 6 giờ và máy \({M_2}\) làm việc không quá 4 giờ nên ta có hệ bất phương trình: \(\left\{ {\begin{array}{*{20}{c}}{3x + y \le 6}\\{x + y \le 4}\\{x,y \ge 0}\end{array}} \right.\) (*).
Số tiền lãi một ngày của phân xưởng này là f(x;y) = 2x + 2,6y (triệu đồng).
Bài toán trở thành tìm giá trị lớn nhất của hàm số f(x;y) trên miền nghiệm của hệ bất phương trình (*).
Miền nghiệm của hệ bất phương trình (*) là tứ giác OABC (kể cả biên).
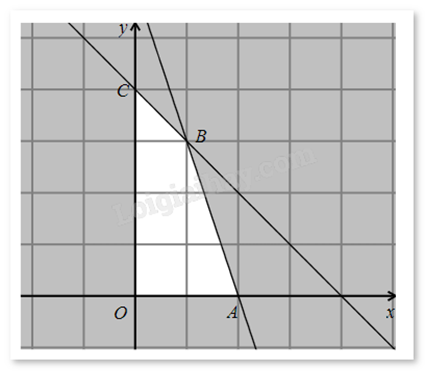
Hàm số f(x;y) sẽ đạt giá trị lớn nhất trên miền nghiệm của hệ bất phương trình (*) khi (x;y) là tọa độ một trong các đỉnh O(0;0), A(2;0), B(1;3), C(0;4).
Thay tọa độ từng điểm vào f(x;y) thấy hàm số đạt giá trị lớn nhất bằng 6,8 khi (x;y) = (1;3).
Vậy số tiền lãi lớn nhất mà phân xưởng này có thể thu được trong một ngày là 6,8 triệu đồng.