Một sợi dây đàn hồi có sóng dừng, biên độ tại bụng sóng là — Không quảng cáo

Tần số dao động: \(f = \frac{\omega }{{2\pi }} = \frac{{2{\rm{0}}\pi }}{{2\pi }} = 1{\rm{0}}Hz\)

Bước sóng: \(\lambda  = \frac{v}{f} = \frac{{24{\rm{0}}}}{{1{\rm{0}}}} = 24cm\)

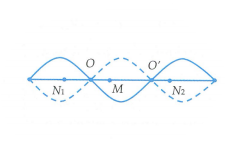
Xét bốn điểm thuộc 3 bó sóng liên tiếp theo thứ tự: Điểm N ₁ thuộc bó sóng thứ nhất - nút O - điểm M gần O nhất thuộc bó sóng thứ 2 - nút O'- điểm N ₂ thuộc bó sóng thứ ba (hình vẽ).

Do biên độ dao động tại M là \({A_M} = \frac{{{A_{\rm{0}}}}}{{\sqrt 2 }}\) nên khoảng cách ngắn nhất từ M tới nút O là: \(MO = \frac{\lambda }{8} = 3cm\)

Với điểm N ₁ nằm bên trái điểm M, ta có \({N_1}O = {N_1}M - MO = 11 - 3 = 8cm\):

\({A_{{N_1}}} = \left| {{A_{\rm{0}}}\sin 2\pi \frac{{{N_1}O}}{\lambda }} \right| = \left| {{A_{\rm{0}}}\sin 2\pi \frac{8}{{24}}} \right| = \frac{{{A_{\rm{0}}}\sqrt 3 }}{2}\)

Điểm N ₁ đồng pha với điểm M nên phương trình dao động của điểm N ₁ là:

\({u_{{N_1}}} = \frac{{{A_{\rm{0}}}\sqrt 3 }}{2}\cos \left( {2{\rm{0}}\pi t + \frac{\pi }{4} - \pi } \right) = \frac{{{A_{\rm{0}}}\sqrt 3 }}{2}\cos \left( {2{\rm{0}}\pi t - \frac{{3\pi }}{4}} \right)\)

Với điểm N ₂ nằm bên phải điểm M, ta có: \({N_2}O' = {N_2}M - MO' = 11 - 9 = 2cm\)

\({A_{{N_2}}} = \left| {{A_{\rm{0}}}\sin 2\pi \frac{{{N_2}O'}}{\lambda }} \right| = \left| {{A_{\rm{0}}}\sin 2\pi \frac{2}{{24}}} \right| = \frac{{{A_{\rm{0}}}}}{2}\)

Điểm N ₂ đồng pha với điểm M nên phương trình dao động của điểm N ₂ là:

\({u_{{N_1}}} = \frac{{{A_{\rm{0}}}}}{2}\cos \left( {2{\rm{0}}\pi t - \frac{{3\pi }}{4}} \right)\)

Đáp án B.