Một sợi dây đàn hồi đang có sóng dừng. Trên dây, những — Không quảng cáo

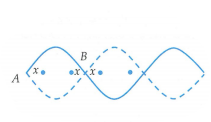
- Các điểm dao động cùng biên độ khi các điểm đó cách nút một khoảng như nhau.

- Giả sử những điểm dao động cùng biên độ cách nút một khoảng x, $x \le \frac{\lambda }{4}$.

- Vì các điểm này có vị trí cân bằng liên tiếp và cách đều nhau, nên từ hình vẽ, ta có: $\left\{ \begin{array}{l}x + d + x = \frac{\lambda }{2}\\x + x = d\end{array} \right. \Rightarrow \left\{ \begin{array}{l}d = \frac{\lambda }{4}\\x = \frac{\lambda }{8}\end{array} \right.$

Vì A ₁ > A ₂ > 0 nên ta có

+ Khi $x = \frac{\lambda }{8}$ thì ta có những điểm có cùng biên độ A ₂ và có vị trí cân bằng cách đều nhau một khoảng ${d_2} = \frac{\lambda }{4}$

Khi $x = \frac{\lambda }{4}$ thì ta có những điểm cùng biên độ A ₁ (điểm bụng) và có vị trí cân bằng cách đều nhau một khoảng ${d_1} = 2x = \frac{\lambda }{2}$

$\left\{ \begin{array}{l}{d_1} = \frac{\lambda }{2}\\{d_2} = \frac{\lambda }{2}\end{array} \right. \Rightarrow \frac{{{d_1}}}{{{d_2}}} = \frac{{\frac{\lambda }{2}}}{{\frac{\lambda }{4}}} = 2 \Rightarrow {d_1} = 2{d_2}$

Đáp án D.