Một vật có khối lượng 2 kg làm bằng vật liệu có khối lượng riêng \(5000{\rm{\;kg}}/{{\rm{m}}^3}\) được treo bởi một lò xo độ cứng \({\rm{k}} = 200{\rm{\;N}}/{\rm{m}}\). Vật được đặt hoàn toàn trong chậu nước, tại vị trí cân bằng vật cách đáy chậu một khoảng \({\rm{h}} = 40{\rm{\;cm}}\). Biết tổng khối lượng của nước là 300 gam , khối lượng riêng và nhiệt dung riêng của nước lần lượt là \(1000{\rm{\;kg}}/{{\rm{m}}^3}\) và \(4200{\rm{\;J}}/{\rm{kg}}\). Nhiệt dung riêng của vật \(250{\rm{\;J}}/{\rm{kg}}.{\rm{K}}\). Lấy gia tốc trọng trường \({\rm{g}} = 10{\rm{\;m}}/{{\rm{s}}^2}\). Cho rằng hệ không trao đổi nhiệt với môi trường bên ngoài, toàn bộ nhiệt lượng mà nước nhận được chỉ để tăng nhiệt độ. Nếu điểm treo bị đứt, độ tăng nhiệt độ của nước bằng
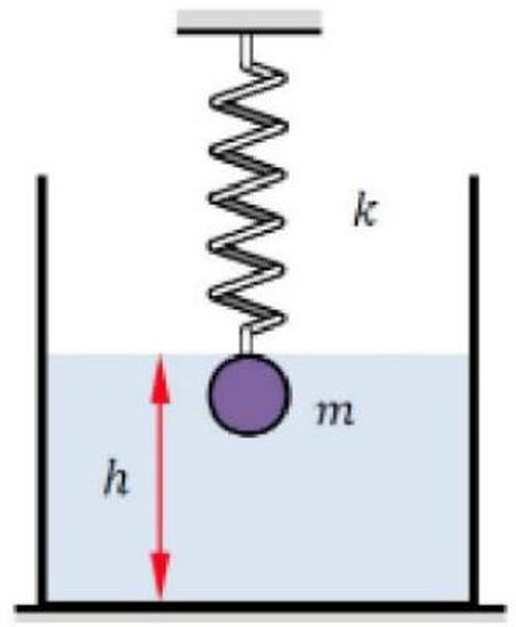
Vận dụng kiến thức về điều kiện cân bằng của vật
Thể tích vật là \({\rm{V}} = \frac{{\rm{m}}}{{\rm{D}}} = \frac{2}{{5000}} = {4.10^{ - 4}}{\rm{\;}}{{\rm{m}}^3}\)
Phương trình điều kiện cân bằng cho vật
\({{\rm{F}}_{\rm{A}}} + {{\rm{F}}_{{\rm{dh}}}} = {\rm{P}} \Rightarrow {{\rm{D}}_{\rm{n}}}{\rm{Vg}} + {\rm{k\Delta }}{\ell _0} = {\rm{mg}} \Rightarrow 1000 \cdot 4 \cdot {10^{ - 4}} \cdot 10 + 200.{\rm{\Delta }}{\ell _0} = 2 \cdot 10 \Rightarrow {\rm{\Delta }}{\ell _0} = 0,08{\rm{\;m}} = 8{\rm{\;cm}}\)
Khi điểm treo bị đứt, thế năng đàn hồi của lò xo và thế năng trọng trường của vật chuyển hóa thành nhiệt. Nước và vật hấp thụ nhiệt và tăng nhiệt độ.
\(\begin{array}{*{20}{r}}{}&{{\rm{Q}} = {{\rm{W}}_{{\rm{dh}}}} + {{\rm{W}}_{\rm{u}}} \Rightarrow \left( {{\rm{m}}{{\rm{c}}_{\rm{v}}} + {{\rm{m}}_{\rm{n}}}{{\rm{c}}_{\rm{n}}}} \right){\rm{\Delta t}} = \frac{1}{2}{\rm{k\Delta }}\ell _0^2 + {\rm{mgh}}}\\{}&{\; \Rightarrow \left( {2.250 + 0,3.4200} \right){\rm{\Delta t}} = \frac{1}{2} \cdot 200 \cdot 0,{{08}^2} + 2 \cdot 10.0,4 \Rightarrow {\rm{\Delta t}} \approx 0,{{0049}^ \circ }{\rm{C}}}\end{array}\)
Đáp án: 0,005