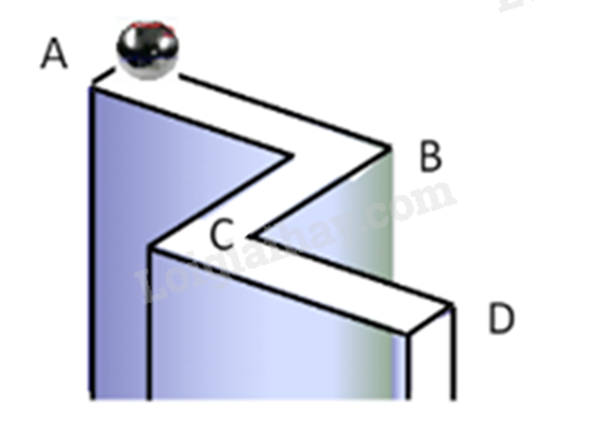
Một viên bi lăn theo đoạn đường từ A đến D như hình vẽ AB — Không quảng cáo

Phương pháp giải

Từ D vẽ $Dx \bot CD$ cắt AB tại E.

Chứng minh BCDE là hình chữ nhật, sử dụng tính chất của hình chữ nhật để tính BE, suy ra độ dài AE.

Dựa vào định lí Pythagore để tính cạnh AD.

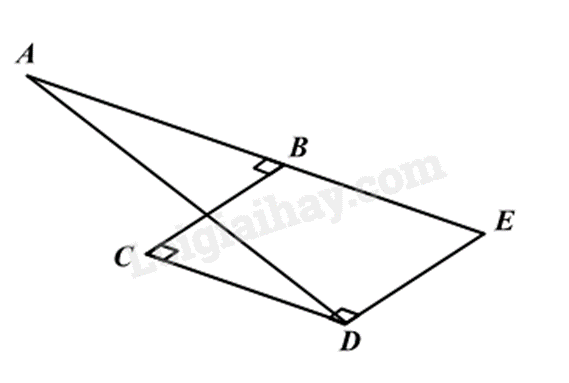
Từ D vẽ $Dx \bot CD$ cắt AB tại E.

Mà $BC \bot CD$ nên $DE//BC$.

Vì $AB \bot BC,BC \bot CD$ nên $AB//CD$.

Xét tứ giác BCDE có $\widehat B = \widehat C = \widehat D = 90^\circ$ nên BCDE là hình chữ nhật.

Suy ra $DE = BC = 12m$; $BE = CD = 6m$; $\widehat E = 90^\circ$.

Dẫn đến $AE = AB + BE = 10 + 6 = 16\left( m \right)$

Áp dụng định lí Pythagore vào tam giác ADE vuông tại E, ta có:

$AD = \sqrt {A{E^2} + D{E^2}}  = \sqrt {{{16}^2} + {{12}^2}}  = 20\left( m \right)$

Vậy khoảng cách AD là 20m.