Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140 kg chất A và 9 kg chất B. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20 kg chất A và 0,6 kg chất B. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng có thể chiết xuất được 10 kg chất A và 1,5 kg chất B. Cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II. Gọi x, y lần lượt là số tấn nguyên liệu loại I và loại II cần dùng.
a) Biểu thức biểu diễn số kg chất A chiết xuất được là 20x + 10y.
b) Biểu thức biểu diễn số kg chất B chiết xuất được là 1,5x + 0,6y.
c) Cặp (x; y) thỏa mãn bài toán thuộc miền nghiệm của hệ \(\left\{ {\begin{array}{*{20}{c}}{2x + y \ge 14}\\\begin{array}{l}5x + 2y \ge 30\\0 \le x \le 9\\0 \le y \le 10\end{array}\end{array}} \right.\).
d) Phải dùng 5 tấn nguyên liệu loại I và 4 tấn nguyên liệu loại II để chi phí nguyên liệu là rẻ nhất.
a) Biểu thức biểu diễn số kg chất A chiết xuất được là 20x + 10y.
b) Biểu thức biểu diễn số kg chất B chiết xuất được là 1,5x + 0,6y.
c) Cặp (x; y) thỏa mãn bài toán thuộc miền nghiệm của hệ \(\left\{ {\begin{array}{*{20}{c}}{2x + y \ge 14}\\\begin{array}{l}5x + 2y \ge 30\\0 \le x \le 9\\0 \le y \le 10\end{array}\end{array}} \right.\).
d) Phải dùng 5 tấn nguyên liệu loại I và 4 tấn nguyên liệu loại II để chi phí nguyên liệu là rẻ nhất.
Lập hệ bất phương trình.
a) Đúng. Biểu thức biểu diễn số kg chất A chiết xuất được là 20x + 10y.
b) Sai. Biểu thức biểu diễn số kg chất B chiết xuất được là 0,6x + 1,5y.
c) Sai. Với số tấn nguyên liệu loại I là x, số tấn nguyên liệu loại II là y, ta có:
Số kg chất A chiết xuất được là 20x + 10y (kg).
Số kg chất B chiết xuất được là 1,5x + 0,6y (kg).
Theo giả thiết ta có \(\left\{ {\begin{array}{*{20}{c}}{20x + 10y \ge 14}\\\begin{array}{l}0,6x + 1,5y \ge 9\\0 \le x \le 9\\0 \le y \le 10\end{array}\end{array}} \right.\) hay \(\left\{ {\begin{array}{*{20}{c}}{2x + y \ge 14}\\\begin{array}{l}2x + 5y \ge 30\\0 \le x \le 9\\0 \le y \le 10\end{array}\end{array}} \right.\).
d) Đúng. Vẽ miền nghiệm của hệ:
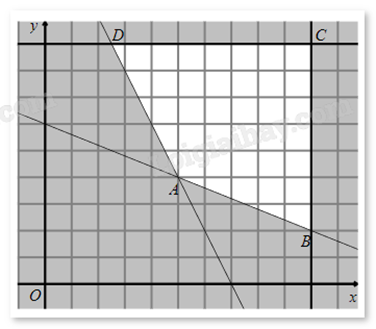
Ta thấy miền nghiệm của hệ là một miền tứ giác ABCD kể cả biên, trong đó A(5;4), B(10;2), C(10;9), \(D\left( {\frac{5}{2};9} \right)\).
Số tiền mua nguyên liệu là P = 4x + 3y.
P đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác. Thay tọa độ các điểm trên vào P, thấy P đạt giá trị nhỏ nhất bằng 32 tại A(5;4).
Vậy, để chi phí nguyên liệu nhỏ nhất, cần mua 5 tấn nguyên liệu loại I và 4 tấn nguyên liệu loại II.