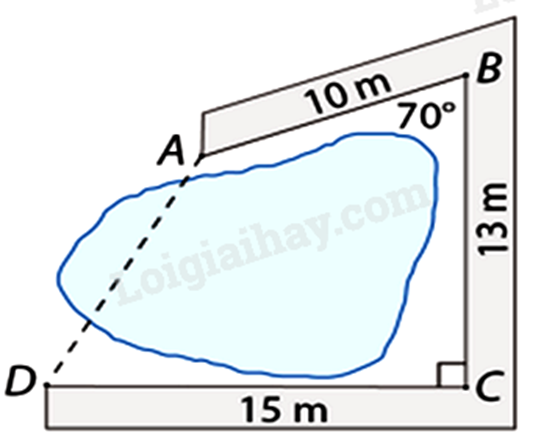
Người ta làm một con đường gồm ba đoạn thẳng AB, BC, CD bao — Không quảng cáo

Phương pháp giải

Vẽ $AK \bot BC$ tại K, $AH \bot DC$ tại H, chứng minh $AK = CH,AH = CK$

Biểu diễn AK, BK theo AB và $\widehat {ABK}$.

Từ đó biểu diễn AH, DH.

Áp dụng định lí Pythagore vào tam giác vuông ADH để tính AD.

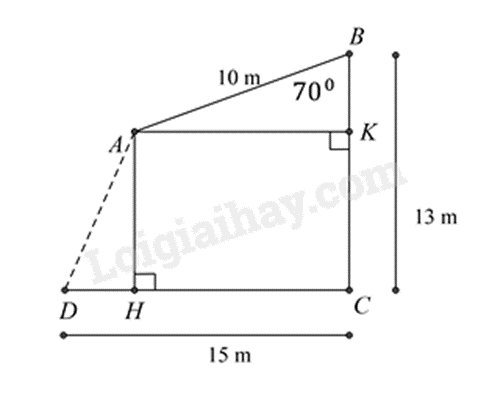
Vẽ $AK \bot BC$ tại K, $AH \bot DC$ tại H, khi đó tứ giác $AKCH$ là hình chữ nhật.

Suy ra $AK = CH,AH = CK$

Trong tam giác vuông $AKB$ vuông tại $K$ có $AB = 10cm$, $\widehat {ABK} = 70^\circ$

+) $AK = AB.\sin 70^\circ  = 10.\sin 70^\circ$

Suy ra $AK = CH = 10.\sin 70^\circ$

Hay $DH = CD - HC = 15 - 10.\sin 70^\circ$

+) $BK = AB.\cos 70^\circ  = 10.\cos 70^\circ$

Suy ra $CK = CB - BK = 13 - 10.\cos {70^0}$

Hay $AH = CK = 13 - 10.\cos 70^\circ$

Theo định lí Pythagore trong tam giác vuông $ADH$, ta có:

$AD = \sqrt {A{H^2} + D{H^2}}  = \sqrt {{{\left( {13 - 10.\cos 70^\circ } \right)}^2} + {{\left( {15 - 10.\sin 70^\circ } \right)}^2}}  \approx 11,1{\rm{ }}m$