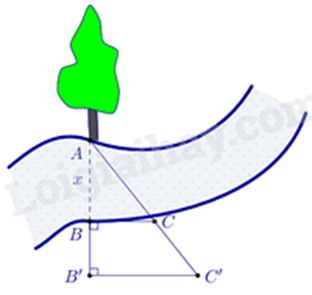
Người ta tiến hành đo đạc các yếu tố cần thiết để tính chiều rộng của một khúc sông mà không cần phải sang bờ bên kia sông (hình vẽ bên). Biết \(BB' = 20\)m, \(BC = 30\)m và \(B'C' = 40\)m. Tính độ rộng \(x\) của khúc sông.
Áp dụng định lí của tam giác bằng nhau, chứng minh $\Delta ABC\backsim \Delta AB'C'$.
Từ đó suy ra tỉ số bằng nhau giữa các cặp cạnh tương ứng.
Ta có: \(\widehat B = \widehat {B'} = {90^0} \Rightarrow \) BC // B’C’. Áp dụng định lí hai tam giác đồng dạng, ta có $\Delta ABC\backsim \Delta AB'C'$.
\( \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\)
\(\frac{x}{{x + 20}} = \frac{{30}}{{40}} = \frac{3}{4}\)
\(\begin{array}{l} \Rightarrow 4x = 3\left( {x + 20} \right)\\4x = 3x + 60\\x = 60\left( m \right)\end{array}\)
Vậy độ rộng x của khúc sông là 60m.