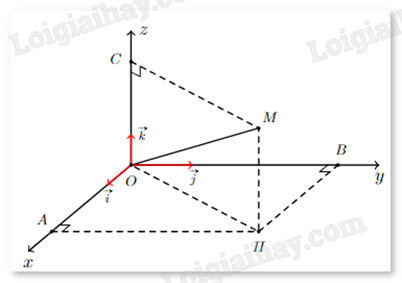
Ở một sân bay, vị trí của máy bay được xác định bởi điểm M trong không gian Oxyz như hình bên. Gọi H là hình chiếu vuông góc của M xuống mặt phẳng (Oxy). Cho biết OM = 50, \(\left( {\overrightarrow i ,\overrightarrow {OH} } \right) = {64^o}\), \(\left( {\overrightarrow {OH} ,\overrightarrow {OM} } \right) = {48^o}\). Biết tọa độ của điểm M là (a;b;c), a, b, c được làm tròn đến hàng phần chục. Tính a + b – c.
Đáp án:
Đáp án:
Điểm M có hoành độ bằng OA, tung độ bằng OB, cao độ bằng OC.
Sử dụng hệ thức lượng trong tam giác để tìm OA, OB, OC.
Ta có:
\(c = OC = OM.\sin {48^o} = 50.\sin {48^o} \approx 37,2\).
\(a = OA = OH.\cos {64^o} = OM.\cos {48^o}.\cos {64^o} = 50.\cos {48^o}.\cos {64^o} \approx 14,7\).
\(b = OB = OH.\sin {64^o} = OM.\cos {48^o}.\sin {64^o} = 50.\cos {48^o}.\sin {64^o} \approx 30,1\).
Vậy a + b – c = 14,7 + 30,1 – 37,2 = 7,6.