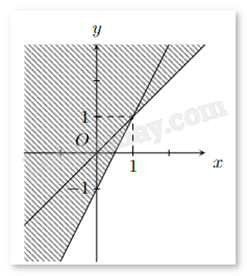
Phần không tô đậm (không kể biên) trong hình vẽ sau biểu diễn miền nghiệm của hệ bất phương trình nào trong các hệ bất phương trình cho dưới đây?
-
A.
\(\left\{ {\begin{array}{*{20}{c}}{x - y \ge 0}\\{2x - y \ge 1}\end{array}} \right.\)
-
B.
\(\left\{ {\begin{array}{*{20}{c}}{x - y > 0}\\{2x - y > 1}\end{array}} \right.\)
-
C.
\(\left\{ {\begin{array}{*{20}{c}}{x - y < 0}\\{2x - y > 1}\end{array}} \right.\)
-
D.
\(\left\{ {\begin{array}{*{20}{c}}{x - y < 0}\\{2x - y < 1}\end{array}} \right.\)
Xét miền nghiệm có chứa biên hay không.
Thay tọa độ của điểm bất kì vào hệ bất phương trình xem có thỏa mãn không.
Dùng phương pháp loại trừ.
Do miền nghiệm không chứa biên nên ta loại đáp án A.
Lấy điểm M(0;1) không thuộc miền nghiệm của cả hai bất phương trình trong hệ bất phương trình, thay tọa độ điểm M vào đáp án B, C, D, nếu không thỏa mãn cả hai bất phương trình trong hệ thì đáp án đúng.
Xét đáp án B, ta thấy \(\left\{ {\begin{array}{*{20}{c}}{0 - 1 = - 1 > 0}\\{2.0 - 1 = 1 > 1}\end{array}} \right.\) không thỏa mãn cả hai bất phương trình. Chọn B.
Xét đáp án C, ta thấy \(\left\{ {\begin{array}{*{20}{c}}{0 - 1 = - 1 < 0}\\{2.0 - 1 = 1 > 1}\end{array}} \right.\) thỏa mãn một bất phương trình. Loại C.
Xét đáp án D, ta thấy \(\left\{ {\begin{array}{*{20}{c}}{0 - 1 = - 1 < 0}\\{2.0 - 1 = 1 < 1}\end{array}} \right.\) thỏa mãn một bất phương trình. Loại D.
Đáp án : B