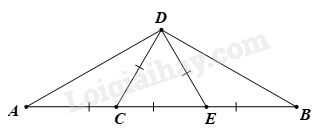
Số đo góc B trong hình vẽ sau là — Không quảng cáo

Phương pháp giải

Tổng ba góc trong một tam giác bằng 180 ⁰ . Tam giác đều có các góc bằng nhau và bằng 60 ⁰ .

Xét tam giác CDE có CD = DE = EC nên tam giác CDE đều. Do đó $\widehat {CDE} = \widehat {DEC} = \widehat {DCE} = {60^0}$.

Góc DEB là góc ngoài đỉnh E của tam giác CDE nên $\widehat {DEC} + \widehat {DEB} = {180^0}$ (hai góc kề bù). Suy ra $\widehat {DEB} = {180^0} - {60^0} = {120^0}$.

Tam giác DEB cân tại E (vì DE = EB).

Xét tam giác DEB cân tại E có $\widehat {DEB} = {120^0}$ nên $\widehat {BDE} = \widehat B = \frac{{{{180}^0} - {{120}^0}}}{2} = {30^0}$.