Tam giác ABC cân tại A, hai đường cao AH và BK, cho BC = — Không quảng cáo

Chứng minh \(\Delta AHC \backsim \Delta BKC\) ( g – g )\( \Rightarrow \frac{{AH}}{{BK}} = \frac{{CA}}{{CB}}\,\,\,\, \Leftrightarrow BK = \frac{{AH.CB}}{{CA}} = \frac{{4.6}}{5} = 4,8\left( {{\rm{cm}}} \right)\,\)

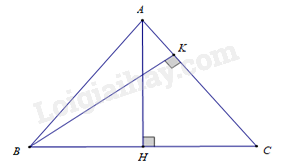
Ta có \(\Delta ABC\) cân tại \(A\) \( \Rightarrow AC = AB = 5\,\left( {{\rm{cm}}} \right)\).

Vì \(\Delta ABC\) cân tại \(A\) nên \(AH\) là đường cao đồng thời là đường trung tuyến ứng với cạnh \(BC\) \( \Rightarrow HB = HC = \frac{{BC}}{2} = \frac{6}{2} = 3\,\left( {{\rm{cm}}} \right)\).

Áp dụng định lí Pytago vào tam giác vuông \(ABH\) ta có:

\(A{H^2} = A{B^2} - H{B^2} = {5^2} - {3^2} = 16\) \( \Rightarrow AH = 4\,\left( {{\rm{cm}}} \right)\)

Xét \(\Delta AHC\) và \(\Delta BKC\) có: góc \(C\) chung; \(\widehat {AHC} = \widehat {BKC} = 90^\circ \).

Nên \(\Delta AHC \backsim \Delta BKC\) ( g – g )\( \Rightarrow \frac{{AH}}{{BK}} = \frac{{CA}}{{CB}}\,\,\,\, \Leftrightarrow BK = \frac{{AH.CB}}{{CA}} = \frac{{4.6}}{5} = 4,8\left( {{\rm{cm}}} \right)\,\).