Tam giác ABC có Â = 60 0 , các tia phân giác của góc B và C cắt nhau tại I. Các tia phân giác góc ngoài tại đỉnh B và C cắt nhau tại K. Tính các góc \(\widehat {BIC}{;^{}}\widehat {BKC}\)
-
A.
\(\widehat {BIC} = {100^o}{;^{}}\widehat {BKC} = {80^o}\)
-
B.
\(\widehat {BIC} = {90^o}{;^{}}\widehat {BKC} = {90^o}\)
-
C.
\(\widehat {BIC} = {60^o}{;^{}}\widehat {BKC} = {120^o}\)
-
D.
\(\widehat {BIC} = {120^o}{;^{}}\widehat {BKC} = {60^o}\)
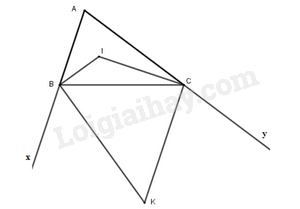
Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat {ABC} + \widehat {BCA} = {180^o}\\ \Rightarrow \widehat {ABC} + \widehat {BCA} = {120^o}\end{array}\)
Vì BI là phân giác \(\widehat {BAC} \Rightarrow \widehat {CBI} = \frac{1}{2}\widehat {BAC}\)
Vì CI là phân giác \(\widehat {BCA} \Rightarrow \widehat {BCI} = \frac{1}{2}\widehat {BCA}\)
Từ đó:
\(\widehat {CBI} + \widehat {BCI} = \frac{1}{2}\left( {\widehat {BAC} + \widehat {BCA}} \right) = \frac{1}{2}{.120^o} = {60^o}\)
Xét tam giác BCI có:
\(\widehat {BCI} + \widehat {BIC} + \widehat {CBI} = {180^o}\)
Nên: \(\widehat {BIC} = {180^o} - \left( {\widehat {BCI} + \widehat {CBI}} \right) = {180^o} - {60^o} = {120^o}\)
Vì BI là phân giác \(\widehat {BAC} \Rightarrow \widehat {CBI} = \frac{1}{2}\widehat {BAC}\)
Vì BK là phân giác \(\widehat {CB{{x}}} \Rightarrow \widehat {CBK} = \frac{1}{2}\widehat {CBx}\)
Suy ra:
\(\widehat {CBK} + \widehat {CBI} = \frac{1}{2}\left( {\widehat {CBx} + \widehat {ABC}} \right) = \frac{1}{2}{.180^o} = {90^o}\)
Hay \(\widehat {IBK} = {90^o}\)
Tương tự ta có: \(\widehat {ICK} = {90^o}\)
Xét tứ giác BICK có:
\(\begin{array}{l}\widehat {BIC} + \widehat {IBC} + \widehat {ICK} + \widehat {BKC} = {360^o}\\ \Rightarrow \widehat {BKC} = {360^o} - {90^o} - {90^o} - {120^o} = {60^o}\end{array}\)
Vậy \(\widehat {BIC} = {120^o}{;^{}}\widehat {BKC} = {60^o}\)
Đáp án : D