Đề bài
Tam giác ABC có M, N lần lượt là trung điểm của AB, AC. Vẽ ME, NF cùng vuông góc với BC (E, F thuộc BC). Khẳng định sai là:
-
A.
MN // EF.
-
B.
ME = NF.
-
C.
MN = ME.
-
D.
MN = EF.
Phương pháp giải
Dựa vào kiến thức về đường trung bình trong tam giác và dấu hiệu nhận biết hình học.
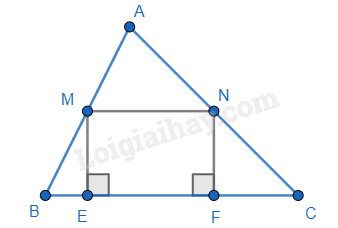
Ta có M, N lần lượt là trung điểm của AB, AC nên MN là đường trung bình của tam giác ABC nên MN // BC và MN = \(\frac{1}{2}\)BC. => MN // EF (E,F \( \in \) BC) nên A đúng.
Ta có ME \( \bot \) BC, NF \( \bot \) BC => ME // NF.
Tứ giác MNFE có MN // EF (E,F \( \in \) BC); ME // NF nên MNFE là hình bình hành.
=> MN = EF; ME = NF (cặp cạnh tương ứng) nên B và D đúng.
MN = ME không có đủ điều kiện để xác định nên C sai.
Đáp án : C