Tam giác ABC vuông tại A có góc B = 60 độ , BD là phân — Không quảng cáo

Phương pháp giải

Chứng minh $\Delta ABC\, \backsim \,\Delta ADB$ ( g – g ) suy ra tỉ số các cạnh từ đó tính độ dài của cạnh BD.

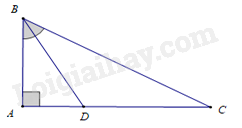
$\Delta ABC$ có $\widehat A = 90^\circ$ nên $\widehat B + \widehat C = 90^\circ  \Rightarrow \widehat {ACB} = 30^\circ$.

Vì $BD$ là phân giác của $\widehat B$ nên $\widehat {ABD} = \widehat {DBC} = \frac{1}{2}\widehat {ABC} = 30^\circ$.

Xét $\Delta ABC$ và $\Delta ADB$ có: $\widehat {ACB} = \widehat {ABD} = 30^\circ$; $\widehat A$ chung

Nên $\Delta ABC \backsim \Delta ADB$ ( g – g ) $\Rightarrow \frac{{BC}}{{BD}} = \frac{{AC}}{{AB}} \Leftrightarrow BD = \frac{{AB.BC}}{{AC}}$.

Xét $\Delta ABC$ có $\widehat A = 90^\circ$, $\widehat C = 30^\circ$ nên $\Delta ABC$ là nửa tam giác đều $\Rightarrow BC = 2AB$.

Áp dụng định lí Pytago vào $\Delta ABC$ có:

$B{C^2} = A{B^2} + A{C^2} \Leftrightarrow {\left( {2AB} \right)^2} = A{B^2} + {18^2} \Leftrightarrow 3A{B^2} = 324 \Leftrightarrow AB = \sqrt {108} \,{\rm{cm}}$.

$\Rightarrow BC = 2\sqrt {108} \,{\rm{cm}}$. Từ đó $BD = \frac{{AB.BC}}{{AC}} = \frac{{\sqrt {108} .2\sqrt {108} }}{{18}} = 12\,({\rm{cm)}}$.