Đề bài
Tam giác ABC vuông tại A. Trên các cạnh AB ,AC lấy các điểm D, E sao cho
BD = CE. Gọi I, K, M, N theo thứ tự là các điểm thuộc các cạnh DE, BE, CB, CD sao cho \(IK = MN = \frac{1}{2}BD,KM = IN = \frac{1}{2}CE\); IK // BD, IN //CE. Tứ giác IKMN là hình gì?
-
A.
Hình vuông.
-
B.
Hình chữ nhật.
-
C.
Hình bình hành.
-
D.
Hình thoi.
Phương pháp giải
Dựa vào các dấu hiệu của hình vuông để chứng minh tứ giác IKMN là hình vuông.
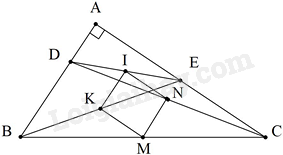
Ta có: \(IK = MN = \frac{1}{2}BD,KM = IN = \frac{1}{2}CE\)
Mà BD = CE nên IK = KM = MN = IN (1)
Lại có: IK // BD, IN //CE
Mặt khác: \(BD \bot CE\)
\( \Rightarrow IK \bot IN(2)\)
Từ (1) và (2) suy ra IKMN là hình vuông.
Đáp án : A