Tam giác ABH vuông tại H có AB = 20cm,BH = 12cm. Trên tia — Không quảng cáo

Phương pháp giải

Sử dụng kiến thức trường hợp đồng dạng thứ nhất của tam giác vuông: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác kia thì hai tam giác vuông đó đồng dạng với nhau.

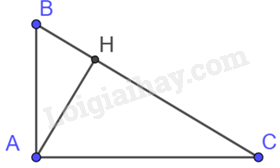
Ta có: \(\frac{{AB}}{{BH}} = \frac{{20}}{{12}} = \frac{5}{3};AC = \frac{5}{3}AH \Rightarrow \frac{{AC}}{{AH}} = \frac{5}{3} \Rightarrow \frac{{AB}}{{BH}} = \frac{{AC}}{{AH}} \Rightarrow \frac{{AB}}{{AC}} = \frac{{BH}}{{AH}}\)

Tam giác ABH và tam giác CAH có: \(\widehat {AHB} = \widehat {AHC} = {90^0},\frac{{AB}}{{AC}} = \frac{{BH}}{{AH}}\)

Do đó, \(\Delta ABH \backsim \Delta CAH\)

Suy ra: \(\widehat {CAH} = \widehat {ABH}\)

Mà \(\widehat {BAH} + \widehat {ABH} = {90^0}\) nên \(\widehat {BAH} + \widehat {CAH} = {90^0}\) hay \(\widehat {BAC} = {90^0}\)