(Thi vào 6 trường Cầu Giấy năm 2019 – 2020)
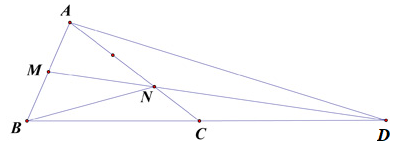
Cho hình tam giác ABC. Lấy M trên AB và N trên AC sao cho AM = BM và NC x 2 = NA.
a) Tính tỉ số diện tích ANM và BMNC
b) Cho MN cắt BC ở D. So sánh BC với CD.
a) $\frac{{{S_{AMN}}}}{{{S_{ABC}}}} = \frac{{AM}}{{AB}} \times \frac{{AN}}{{AC}} = \frac{1}{2} \times \frac{2}{3} = \frac{1}{3}$
$ \Rightarrow \frac{{{S_{BMNC}}}}{{{S_{ABC}}}} = \frac{2}{3}$
Suy ra $\frac{{{S_{AMN}}}}{{{S_{BMNC}}}} = \frac{1}{2}$
b) Nối A với D
Ta có ${S_{AMD}} = {S_{BMD}}$ (Chung chiều cao hạ từ D và MA = MB)
Ta có ${S_{AMN}} = {S_{BMN}}$ (Chung chiều cao hạ từ N và MA = MB)
Suy ra ${S_{AND}} = {S_{BND}}$
Lại có ${S_{CND}} = \frac{1}{2}{S_{AND}}$ (Chung chiều cao hạ từ D và xuống đáy AC và đáy $NC = \frac{1}{2}NA$)
Suy ra ${S_{CND}} = \frac{1}{2}{S_{BND}}$. Mà hai tam giác này chung chiều cao hạ từ N xuống BD nên $CD = \frac{1}{2}BD$
Vậy BC = CD