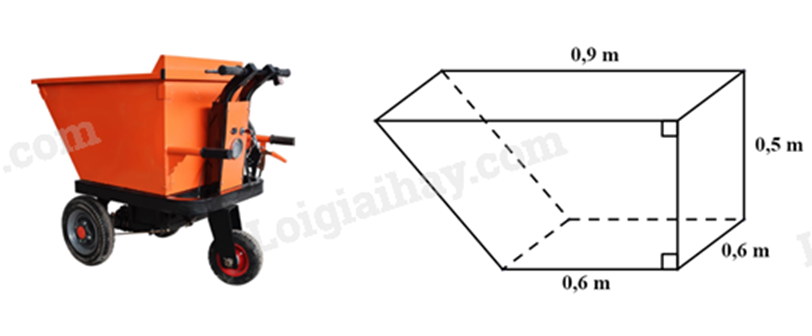
Thùng của một xe rùa điện có dạng hình lăng trụ đứng tứ giác; mặt đáy của hình lăng trụ này là một hình thang vuông có độ dài đáy lớn, đáy nhỏ và chiều cao lần lượt là \(0,9m\); \(0,6m\) và \(0,5m\), chiều cao của hình lăng trụ là \(0,6m\) (xem hình vẽ bên dưới) . Để đảm bảo an toàn cho bác công nhân chở cát, mỗi chuyến xe chỉ vận chuyển được \(96\% \) thể tích của thùng xe. Hỏi bác công nhân phải vận chuyển ít nhất bao nhiêu chuyến xe để chở hết \(54{m^3}\) cát?
Sử dụng công thức tính thể tích hình lăng trụ đứng tứ giác.
Tính thể tích cát của mỗi chuyến xe.
Từ đó tính số chuyến xe ít nhất để vận chuyển hết cát.
Thể tích của thùng xe là:
\(\frac{{\left( {0,9 + 0,6} \right).0,5}}{2}.0,6 = 0,225\,\left( {{m^3}} \right)\)
Thể tích cát của mỗi chuyến xe là:
\(0,225.96\% = 0,216\,\left( {{m^3}} \right)\)
Ta có: \(54:0,216\, = 250\).
Vậy cần ít nhất 250 chuyến xe để có thể vận chuyển hết \(54\,{m^3}\) cát.