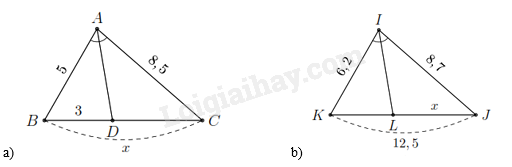
1. Tính \(x\) trong hình và làm tròn kết quả đến hàng phần mười.
2. Hình thang ABCD (AB // CD) có DC = 2AB. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
a) Chứng minh các tứ giác ABPD, MNPQ là hình bình hành.
b) Tìm điều kiện của hình thang ABCD để MNPQ là hình thoi.
c) Gọi E là giao điểm của BD và AP. Chứng minh ba điểm Q, N, E thẳng hàng.
1. Dựa vào tính chất đường phân giác, sử dụng tỉ số bằng nhau để tính.
2.
a) Dựa vào dấu hiệu nhận biết hình bình hành và tính chất đường trung bình để chứng minh.
b) Dựa vào dấu hiệu nhận biết hình thoi và tính chất đường trung bình.
c) Sử dụng tính chất đường trung bình để chứng minh EQ // AB và EN // AB suy ra Q, N, E thẳng hàng.
1.
a)
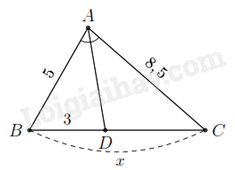
Do \(AD\) là đường phân giác trong của góc \(A\) nên ta có
\(\frac{{DC}}{{DB}} = \frac{{AC}}{{AB}} \Rightarrow DC = \frac{{AC}}{{AB}} \cdot DB.\)
Thay số ta có \(DC = \frac{{8,5}}{5} \cdot 3 = 5,1\). Khi đó \(x = DB + DC = 3 + 5,1 = 8,1\).
b)
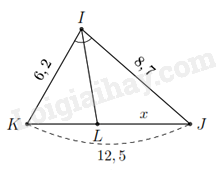
Với \(KL = 12,5 - x\) và do \(IL\) là đường phân giác trong của góc \(I\) nên theo tính chất đường phân giác ta có
Theo tính chất đường phân giác ta có
\(\frac{{KL}}{{LJ}} = \frac{{IK}}{{IJ}} \Rightarrow \frac{{12,5 - x}}{x} = \frac{{6,2}}{{8,7}} \Leftrightarrow x = \frac{{2175}}{{298}} \approx 7,3\).
2.
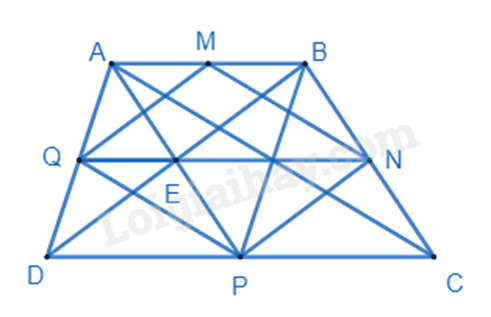
a) Ta có: \(DP = \frac{1}{2}DC = AB\); \(AB//CD \Rightarrow AB//DP\) nên ABPD là hình bình hành.
Vẽ AC, ta có MN là đường trung bình \(\Delta ABC \Rightarrow MN = \frac{1}{2}AC;MN//AC\).
Chứng minh tương tự \( \Rightarrow PQ = \frac{1}{2}AC;PQ//AC\).
\( \Rightarrow MN = PQ;PQ//AC\) nên MNPQ là hình bình hành.
b)
Tương tự như đường chéo AC, vẽ BD, ta cũng chứng minh được MQ và NP là đường trung bình của tam giác ABD và BCD nên \(MQ = NP = \frac{1}{2}BD;MQ//NP//BD\).
MNPQ là hình thoi khi MN = MQ mà \(MN = \frac{1}{2}AC;MQ = \frac{1}{2}BD\) (tính chất đường trung bình)
\( \Rightarrow AC = BD\). Khi đó ABCD là hình thang cân.
c) Vì ABPD là hình bình hành nên E là trung điểm của AP.
Xét tam giác ABD có QE là đường trung bình của tam giác ABD nên QE // AB (1)
Xét tam giác DBC có EN là đường trung bình của tam giác DBC nên EN // DC mà DC // AB nên EN // AB (2)
Từ (1) và (2) suy ra từ E kẻ được EQ // AB và EN // AB nên Q, E, N thẳng hàng