Toán lớp 5 trang 112 Luyện tập
Tính diện tích xung quanh và diện tích toàn phần của hình lập phương có cạnh 2m 5cm. Mảnh bìa nào dưới đây có thể gấp được một hình lập phương ?
Bài 1
Tính diện tích xung quanh và diện tích toàn phần của hình lập phương có cạnh 2m 5cm.
Phương pháp giải:
Áp dụng các công thức:
Diện tích xung quanh = diện tích một mặt \(\times \) 4 = cạnh \(\times \) cạnh \(\times \) 4.
Diện tích toàn phần = diện tích một mặt \(\times \) 6 = cạnh \(\times \) cạnh \(\times \) 6.
Lời giải chi tiết:
Đổi: 2m 5cm = 2,05m
Diện tích xung quanh của hình lập phương đã cho là:
(2,05 \(\times \) 2,05) \(\times \) 4 = 16,81 (m 2 )
Diện tích toàn phần của hình lập phương đã cho là:
(2,05 \(\times \) 2,05) \(\times \) 6 = 25,215 (m 2 )
Đáp số: Diện tích xung quanh: 16,81m 2 ;
Diện tích toàn phần: 25,215m 2 .
Bài 2
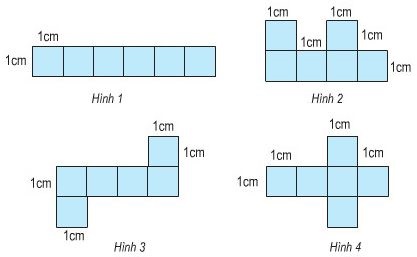
Mảnh bìa nào dưới đây có thể gấp được một hình lập phương ?
Phương pháp giải:
Cách 1: Học sinh vẽ hình lên giấy rồi gấp thử và trả lời.
Cách 2: Học sinh suy luận để trả lời.
Lời giải chi tiết:
Cách 1: Học sinh vẽ hình lên giấy rồi gấp thử và trả lời.
Cách 2: Suy luận:
- Dễ thấy không thể gấp hình 1 thành một hình lập phương.
- Với hình 2, khi ta gấp dãy 4 hình vuông ở dưới thành 4 mặt xung quanh thì 2 hình vuông ở trên sẽ đè lên nhau, không tạo thành một mặt đáy trên và một mặt đáy dưới được. Do đó không thể gấp hình 2 thành một hình lập phương.
- Hình 3 và hình 4 đều có thể gấp thành hình lập phương vì khi ta gấp dãy 4 hình vuông ở giữa thành 4 mặt xung quanh thì 2 hình vuông trên và dưới sẽ tạo thành hai mặt đáy trên và đáy dưới.
Vậy mỗi mảnh bìa ở hình 3 và hình 4 đều có thể gấp thành một hình lập phương.
Bài 3
Đúng ghi Đ, sai ghi S:
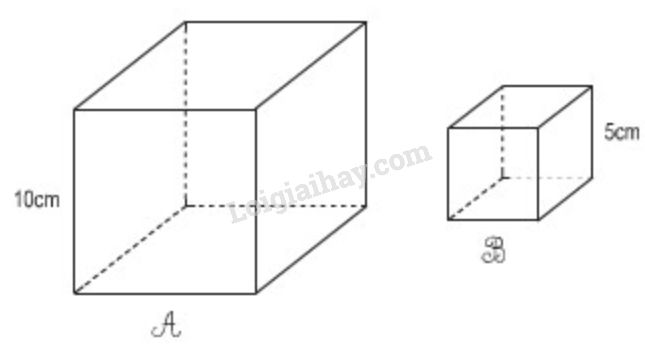
a) Diện tích xung quanh của hình lập phương A gấp 2 lần diện tích xung quanh của hình lập phương B
b) Diện tích xung quanh của hình lập phương A gấp 4 lần diện tích xung quanh của hình lập phương B.
c) Diện tích toàn phần của hình lập phương A gấp 2 lần diện tích toàn phần của hình lập phương B.
d) Diện tích toàn phần của hình lập phương A gấp 4 lần diện tích toàn phần của hình lập phương B.
Phương pháp giải:
- Tính diện tích xung quanh và diện tích từng phần của từng hình lập phương rồi so sánh kết quả với nhau:
+ Diện tích xung quanh = diện tích một mặt \(\times \) 4 = cạnh \(\times \) cạnh \(\times \) 4.
+ Diện tích toàn phần = diện tích một mặt \(\times \) 6 = cạnh \(\times \) cạnh \(\times \) 6.
Lời giải chi tiết:
Diện tích xung quanh của hình lập phương A là:
\((10 \times 10) \times 4 = 400 \; (cm^2)\)
Diện tích toàn phần của hình lập phương A là:
\((10 \times 10) \times 6 = 600 \; (cm^2)\)
Diện tích xung quanh của hình lập phương B là:
\((5 \times 5) \times 4 = 100 \; (cm^2)\)
Diện tích toàn phần của hình lập phương B là:
\((5 \times 5) \times 6 = 150 \; (cm^2)\)
Diện tích xung quanh của hình lập phương A gấp diện tích xung quanh của hình lập phương B số lần là:
\(400 : 100 = 4\) (lần)
Diện tích toàn phần của hình lập phương A gấp diện tích toàn phần của hình lập phương B số lần là:
\(600 : 150 = 4\) (lần)
Vậy diện tích xung quanh (toàn phần) của hình A gấp \(4\) lần diện tích xung quanh (toàn phần) của hình B.
Ta có kết quả:
a) S b) Đ c) S d) Đ
Cách giải nhanh: Nếu cạnh hình lập phương này gấp \(n\) lần cạnh hình lập phương kia thì diện tích xung quanh (toàn phần) của hình này gấp \( n \times n\) lần diện tích xung quanh (toàn phần) của hình lập phương kia.