Tổng hợp 10 đề thi giữa kì 1 Toán 7 chân trời sáng tạo có đáp án
I. TRẮC NGHIỆM ( 3 điểm) Chọn chữ cái A,B,C hoặc D đứng trước câu trả lời đúng.
Đề 1
I. TRẮC NGHIỆM ( 3 điểm)
Chọn chữ cái A,B,C hoặc D đứng trước câu trả lời đúng.
Câu 1: Phân số biểu diễn số hữu tỉ -0,6 là:
A. \(\dfrac{6}{{10}}\) B. \(\dfrac{{ - 6}}{1}\) C. \(\dfrac{{ - 12}}{{10}}\) D. \(\dfrac{{18}}{{ - 30}}\)
Câu 2: Kết quả của phép tính: \(\left( {\dfrac{2}{3} - \dfrac{5}{4}} \right):\dfrac{{21}}{{12}}\) là:
A. 3 B. -3 C. -2 D. -4
Câu 3: Giá trị của x trong biểu thức \( - {x^3} = 27\) là:
A. \( \pm 3\) B. \( \pm 9\) C. 3 D. -3
Câu 4: Hình hộp chữ nhật có bao nhiêu cạnh?
A. 4 B. 6 C. 8 D. 12
Câu 5: Thể tích của hình lăng trụ đứng tứ giác có đáy là hình thoi có 2 đường chéo 8 cm, 12 cm; chiều cao 20 cm là:
A. \(96c{m^2}\) B. \(96c{m^3}\) C. \(192c{m^3}\) D. \(192c{m^2}\)
Câu 6: Để dán kín các mặt của hình lập phương cạnh 8 m cần diện tích giấy là bao nhiêu ?
A. \(48{m^2}\) B. \(64{m^2}\)
C. \(512{m^2}\) D. \(384{m^2}\)
II. TỰ LUẬN ( 7 ĐIỂM)
Câu 7: ( 1 điểm) Thực hiện phép tính (tính nhanh nếu có thể).
a) \(\dfrac{{13}}{{25}} - \dfrac{{31}}{{41}} + \dfrac{{12}}{{25}} - \dfrac{{10}}{{41}} - 0,5\)
b) \({( - 2)^3} - {\left( { - \dfrac{1}{2}} \right)^2}:\dfrac{{ - 1}}{{16}} - {2023^0}\)
Câu 8: (1 điểm) Tìm x, biết:
a) \(\dfrac{1}{3}x - \dfrac{2}{5} = \dfrac{{ - 7}}{{15}}\) b) \({2^{x - 3}} - {3.2^x} + 92 = 0\)
Câu 9: (1 điểm)
Vào dịp Tết Nguyên đán, bà Ngọc dự định gói 20 cái bánh chưng cho gia đình. Nguyên liệu làm bánh gồm gạo nếp, đậu xanh, thịt lợn và lá dong. Mỗi cái bánh chưng sau khi gói nặng 0,75 kg gồm 0,45 kg gạo; 0,125 kg đậu xanh, 0,04 kg lá dong, còn lại là thịt. Hỏi khối lượng thịt bà cần chuẩn bị để gói bánh là khoảng bao nhiêu?
Câu 10: (3,5 điểm)
- Một bể nước có dạng hình hộp chữ nhật với chiều dài 3 m. Lúc đầu bể không có nước. Sau khi đổ vào bể 120 thùng nước, mỗi thùng chứa 20 lít nước thì mực nước của bể dâng cao 0,8 m.
a) Tính chiều rộng của bể nước
b) Người ta đổ thêm 60 thùng nước thì đầy bể. Hỏi bể nước cao bao nhiêu mét?
2. Một cái bục lăng trụ đứng có kích thước như hình dưới:
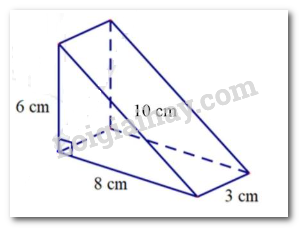
a) Người ta muốn sơn tất cả các mặt của bục. Diện tích cần phải sơn là bao nhiêu?
b) Tính thể tích của cái bục
Câu 11: (0,5 điểm)
Tìm số hữu tỉ x sao cho:
\(\dfrac{{x + 1}}{{2023}} + \dfrac{{x + 2}}{{2022}} = \dfrac{{x + 3}}{{2021}} + \dfrac{{x + 4}}{{2020}}\)
Đề 2
I. TRẮC NGHIỆM ( 3 điểm)
Chọn chữ cái A,B,C hoặc D đứng trước câu trả lời đúng.
Câu 1: Số hữu tỉ là:
A. Phân số khác 0
B. Các số viết được dưới dạng \(\dfrac{a}{b}\left( {a,b \in N,b \ne 0} \right)\)
C. Các số viết được dưới dạng \(\dfrac{a}{b}\left( {a,b \in Z,b \ne 0} \right)\)
D. Các số viết được dưới dạng \(\dfrac{a}{b}\left( {a,b \in Z} \right)\)
Câu 2: Giá trị x thỏa mãn \(27{x^2} - 3 = 0\)là:
A. \(x = \dfrac{1}{9}\); B. \(x = \dfrac{1}{3}\);
C. \(x = 3\) D. \(x = \pm \dfrac{1}{3}\).
Câu 3: Kết quả của phép tính \(\dfrac{{{3^5}{{.4}^4}}}{{{9^2}{{.8}^2}}}\)là
A. \(\dfrac{3}{{16}}\); B. \(1\);
C. \(\dfrac{3}{4}\); D. Một kết quả khác.
Câu 4: Hình lăng trụ đứng tam giác có bao nhiêu mặt?
- 3 B. 5 C. 6 D. 9
Câu 5: Hình lăng trụ đứng tam giác có đáy là tam giác có 3 cạnh đều bằng \(3cm\), chiều cao hình lăng trụ bằng \(10cm\). Diện tích xung quanh của hình lăng trụ đó là:
A. \(30c{m^2}\) B. \(90c{m^2}\) C. \(90c{m^3}\) D. \(13c{m^2}\)
Câu 6: Một bể cá hình lập phương có độ dài cạnh là \(0,8m\), thể tích nước chiếm \(\dfrac{3}{4}\) bể. Hỏi trong bể chứa bao nhiêu lít nước?
A. 348 lít nước B. 384 lít nước C. 405 lít nước D. 400 lít nước
II. TỰ LUẬN ( 7 ĐIỂM)
Câu 7: ( 1 điểm) Tính giá trị của các biểu thức sau:
a) \({\mkern 1mu} {\mkern 1mu} \dfrac{{ - 4}}{{13}}.10\dfrac{3}{{41}} - \dfrac{4}{{13}}.2\dfrac{{38}}{{41}}\) b) \({\mkern 1mu} {\mkern 1mu} \sqrt {25} .\left( {0,4 - 1\dfrac{1}{2}} \right):\left[ {{{\left( { - 2} \right)}^3}.\dfrac{{11}}{8}} \right]\)
Câu 8 : (1,5 điểm)
Tìm x, biết:
a) \(0,2 - x = - 1\dfrac{2}{5}\)
b) \(\dfrac{{x + \dfrac{3}{2}}}{6} = \dfrac{{ - 5}}{{12}}\)
c) \(3.\left( { - 2x + \dfrac{5}{2}} \right).\left( {x + 11} \right) = 0\)
Câu 9: (1 điểm)
Có hai tấn ảnh kích thước 20 cm x 30 cm được in trên giấy ảnh kích thước 43,2 cm x 55,8 cm. Nếu cắt ảnh theo đúng kích thước thì diện tích phần giấy ảnh còn lại là bao nhiêu?
Câu 10: (3,5 điểm)
- Một cái thùng sắt hình hộp chữ nhật có chiều rộng bằng \(\dfrac{5}{8}\) chiều dài và kém chiều dài 3,6 m; chiều cao bằng 2,5 m. Hỏi
a) Diện tích toàn phần của cái thùng
b) Nếu người ta sơn bên ngoài cái thùng, cứ 3,6 m 2 tốn 3 kg sơn thì cần bao nhiêu kg sơn?
2. Người ta đào một đoạn mương có dạng hình lăng trụ đứng tứ giác. Biết mương có chiều dài 30 m, sâu 1,5 m, trên bề mặt có chiều rộng 1,8 m và đáy mương là 1,2 m.
a) Tính diện tích đáy hình thang của hình lăng trụ
b) Tính thể tích đất phải đào lên.
Câu 11: (0,5 điểm)
Cho biểu thức \(A = \dfrac{1}{5} + \dfrac{1}{{{5^2}}} + \dfrac{1}{{{5^3}}} + .... + \dfrac{1}{{{5^{2022}}}}\). Chứng minh \(A < \dfrac{1}{4}\)
Đề 3
I. TRẮC NGHIỆM ( 3 điểm)
Chọn chữ cái A,B,C hoặc D đứng trước câu trả lời đúng.
Câu 1: Điểm biểu diễn của số hữu tỉ \(\dfrac{{ - 3}}{5}\) trên trục số là hình vẽ nào dưới đây?
A.

B.

C.

D.

Câu 2: Kết quả của phép tính: \( - 2,593 - \dfrac{2}{5}\) là:
A. \(2,993\) B. \( - 2,993\) C. \(2,193\) D. \( - 2,193\)
Câu 3: Trong các tập hợp sau, tập hợp nào có tất cả các phần tử đều là số vô tỉ?
A. \(A = \left\{ { - 0,1;\sqrt {12} ;\dfrac{{21}}{{32}}; - 316} \right\}\) B. \(B = \left\{ {32,1;\sqrt {25} ;\sqrt {\dfrac{1}{{16}}} ;\sqrt {0,01} } \right\}\)
C. \(C = \left\{ {\sqrt 3 ;\sqrt 5 ;\sqrt {31} ;\sqrt {83} } \right\}\) D. \(D = \left\{ { - \dfrac{1}{2};\dfrac{{231}}{2};\dfrac{2}{5}; - 3} \right\}\)
Câu 4: Hình hộp chữ nhật có ba kích thước: chiều dài là \(a\), chiều rộng là \(b\), chiều cao là \(c\) (\(a,b,c\) cùng đơn vị đo). Khi đó, diện tích xung quanh của hình hộp chữ nhật được tính theo công thức:
A. \({S_{xq}} = \left( {a + b} \right)c\) B. \({S_{xq}} = 2\left( {a + b} \right)c\) C. \({S_{xq}} = \left( {b + c} \right)a\) D. \({S_{xq}} = 2\left( {b + c} \right)a\)
Câu 5: Tính thể tích hình lăng trụ đứng có đáy là hình thang cân có kích thước như hình bên dưới:
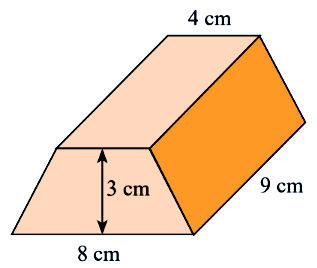
A. \(72c{m^3}\) B. \(162c{m^3}\) C. \(88c{m^3}\) D. \(132c{m^3}\)
Câu 6: Hãy kể tên 4 góc kề với \(\angle AOC\) (không kể góc bẹt) trong hình vẽ dưới đây:
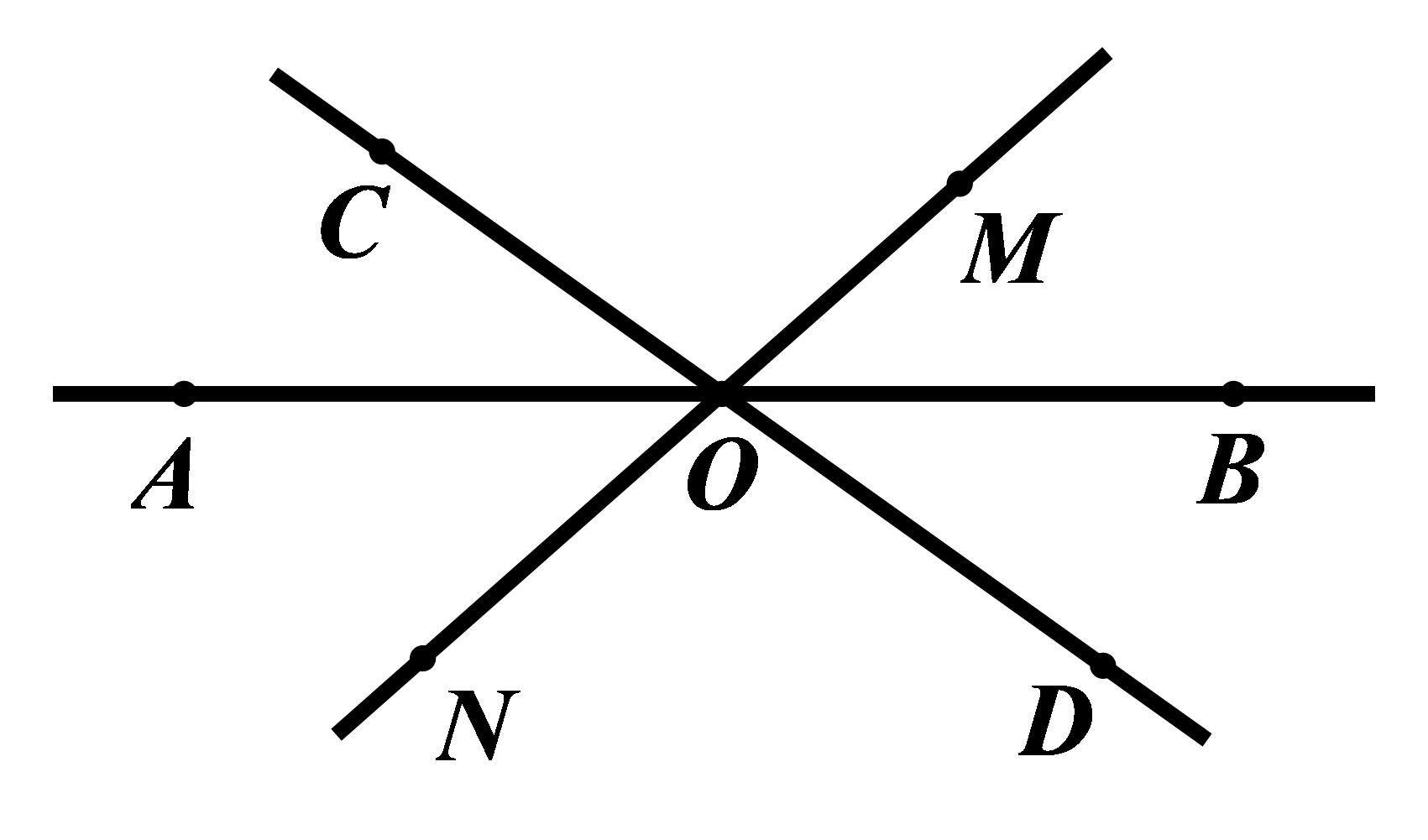
A. \(\angle COM;\angle MOB;\angle AON;\angle DOB\) B. \(\angle COM;\angle COD;\angle AON;\angle MON\)
C. \(\angle COM;\angle COB;\angle AON;\angle AOD\) D. \(\angle COM;\angle MOD;\angle AON;\angle CON\)
Phần II. Tự luận (7 điểm):
Bài 1: (1 điểm)
Sắp xếp các số sau:
a) Theo thứ tự tăng dần: \( - 3,7;\dfrac{{21}}{{11}};1\dfrac{1}{2};\dfrac{{ - 13}}{6};\dfrac{{ - 1}}{5};\dfrac{3}{7}\);
b) Theo thứ tự giảm dần: \(\dfrac{{ - 3}}{{61}};0;\dfrac{{17}}{{48}};2\dfrac{1}{5};2,45;\dfrac{{ - 1}}{{10}}\).
Bài 2: (2,0 điểm)
Tính một cách hợp lí:
a) \(\dfrac{{ - 5}}{6}.\dfrac{7}{{11}} + \dfrac{{ - 5}}{{11}}.\dfrac{4}{6} + \dfrac{5}{6}\) b) \(\left[ {\left( {\dfrac{{ - 3}}{8} + \dfrac{{11}}{{23}}} \right):\dfrac{5}{9} + \left( {\dfrac{{ - 5}}{8} + \dfrac{{12}}{{23}}} \right):\dfrac{5}{9}} \right].\dfrac{{ - 11}}{{325}}\)
c) \(\dfrac{{{{15}^5}}}{{{5^5}}} - {\left( { - 0,25} \right)^2}{.4^2}\) d) \( - \dfrac{{{2^{15}}{{.9}^4}}}{{{6^6}{{.8}^3}}} + 0,75.\dfrac{{ - 1}}{2} + 0,375\)
Bài 3: (2,0 điểm)
Tìm \(x\), biết:
a) \(\left( { - 0,4} \right).\left( {2x + \dfrac{2}{5}} \right) = - 9,4\) b) \(\left( {\dfrac{3}{2} - x} \right):\dfrac{{ - 14}}{3} = - \dfrac{6}{7}\)
c) \(x + 2.\sqrt {16} = - 3.\sqrt {49} \) d) \(2 + \dfrac{1}{6} - x = 10.\sqrt {0,01} - \sqrt {\dfrac{{25}}{{36}}} \)
Bài 4: (1,0 điểm)
Một căn phòng có dạng hình hộp chữ nhật với chiều dài là 6m, chiều rộng là 4,2m, chiều cao là 3,2m. Người ta muốn sơn phía trong bốn bức tường và cả trần của căn phòng. Tính số tiền mà người ta phải trả, biết diện tích của các của của căn phòng là và giá tiền mỗi mét vuông (bao gồm tiền công và nguyên vật liệu) là 12 100 đồng.
Bài 5: (1,0 điểm)
Quan sát hình vẽ bên dưới, có \(\angle COD = {80^0};\angle COE = {60^0}\), tia \(OG\) là tia phân giác của\(\angle COD\).

a) Tính số đo của \(\angle EOG?\)
b) Tia \(OE\) có là tia phân giác của \(\angle DOG\) hay không? Giải thích vì sao?
Đề 4
I. TRẮC NGHIỆM ( 3 điểm)
Chọn chữ cái A,B,C hoặc D đứng trước câu trả lời đúng.
Câu 1: Tìm phát biểu đúng trong các phát biểu sau:
A. \(\dfrac{2}{5} \in \mathbb{Z}\) B. \( - 5 \in \mathbb{N}\) C. \(\dfrac{{ - 5}}{4} \notin \mathbb{Q}\) D. \(\dfrac{3}{2} \in \mathbb{Q}\)
Câu 2: Tìm \(x\), biết: \(\dfrac{1}{2} - \dfrac{2}{3}x = \dfrac{1}{4}\)
A. \(x = \dfrac{{ - 3}}{8}\) B. \(x = \dfrac{3}{8}\) C. \(x = \dfrac{1}{2}\) D. \(x = - 1\)
Câu 3: Kết quả của phép tính: \(\sqrt {1,44} - 2.{\left( {\sqrt {0,6} } \right)^2}\)
A. \(0,24\) B. \(0\) C. \(0,12\) D. \(0,2\)
Câu 4: Cho hình vẽ bên dưới. Biết tia \(Oz\) là tia phân giác của \(\angle xOy\). Tính \(\angle xOy\).

A. \(\angle xOy = {56^0}\) B. \(\angle xOy = {121^0}\) C. \(\angle xOy = {112^0}\) D. \(\angle xOy = {100^0}\)
Câu 5: Trong các hình vẽ dưới đây, liệt kê tất cả các hình là hình lăng trụ đứng tam giác hoặc hình lăng trụ đứng tứ giác?

A. Tất cả 6 hình B. Hình a), c), e), f) C. Hình b), c), d) D. Hình b), d)
Câu 6: Một hình lập phương có thể tích là \(343{m^3}\). Diện tích xung quanh của hình lập phương đó là:
A. \(343{m^2}\) B. \(98{m^2}\) C. \(196{m^2}\) D. \(240{m^2}\)
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm)
Thực hiện phép tính:
a) \(\dfrac{{13}}{{50}}.\left( { - 15,5} \right) - \dfrac{{13}}{{50}}.84\dfrac{1}{2}\) b) \(\dfrac{2}{9} + \dfrac{1}{3}:\left( { - \dfrac{3}{2}} \right) + \dfrac{1}{2}.\left( { - 0,5} \right)\)
c) \(4.{\left( { - \dfrac{1}{2}} \right)^3} - 2.{\left( {\dfrac{{ - 1}}{2}} \right)^2} + 3.\left( { - \dfrac{1}{2}} \right) + 1\) d) \(\dfrac{{{{\left( { - 0,7} \right)}^2}.{{\left( { - 5} \right)}^3}}}{{{{\left( {\dfrac{{ - 7}}{3}} \right)}^3}.{{\left( {\dfrac{3}{2}} \right)}^4}.{{\left( { - 1} \right)}^5}}}\)
Bài 2: (1 điểm)
a) Sắp xếp các số sau theo thứ tự tăng dần: \(6{\kern 1pt} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {46} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} - \sqrt {81} {\kern 1pt} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} - 3,6{\kern 1pt} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} 2.\sqrt {16} \).
b) Sắp xếp các số sau theo thứ tự giảm dần: \(\sqrt {78} {\kern 1pt} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {50 + 4} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} - 8{\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} - 3.\sqrt {0,25} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 6{\kern 1pt} {\kern 1pt} \).
Bài 3: (2,0 điểm)
Tìm \(x\), biết:
a) \({\left( {\dfrac{4}{5}} \right)^6}.x = {\left( {\dfrac{4}{5}} \right)^7}\) b) \({\left( {0,03} \right)^3}:x = - {\left( {0,03} \right)^2}\)
c) \(\sqrt {0,16} + x = 3.\sqrt {0,09} .2\dfrac{1}{3}\) d) \(\sqrt {0,25} - 3x - \sqrt {0,49} .\dfrac{1}{7} = \sqrt {0,04} .\dfrac{1}{2}\)
Bài 4: (1,0 điểm)
Một giá đình xây bể chứa nước hình lăng trụ đứng, phần trong lòng bể có đáy là hình vuông cạnh 1,5m, chiều cao bể là 1m. Sau đó họ dùng các viên gạch men kịch thước \(20 \times 30\)cm, dày 1cm để ốp xung quanh bể và đáy bể. Hỏi gia đình đó cần ít nhất bao nhiêu viên gạch ốp và sau khi ốp bể chứa được khoảng bao nhiêu lít nước?
Bài 5: (1,0 điểm)
Cho \(\angle xOy = {30^0}\), vẽ góc \(\angle xOt = {70^0}\) sao cho tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Ot\).
a) Tính \(\angle yOt?\) Tia \(Oy\) có là tia phân giác của góc \(\angle xOy\) không? Vì sao?
b) Gọi tia \(Om\) là tia đối của tia \(Ox\). Tính số đo của \(\angle mOt?\)
c) Gọi \(Oz\) là tia phân giác của \(\angle mOt\). Tính số đo của \(\angle yOz?\)
Đề 5
I. TRẮC NGHIỆM ( 3 điểm)
Chọn chữ cái A,B,C hoặc D đứng trước câu trả lời đúng.
Câu 1: Lớp 7B có \(\dfrac{4}{5}\) số học sinh thích học toán, \(\dfrac{7}{{10}}\) số học sinh thích học văn, \(\dfrac{{23}}{{25}}\) số học sinh thích học Tiếng Anh. Môn học nào được nhiều bạn học sinh lớp 7B yêu thích nhất?
A. Môn toán B. Môn văn
C. Môn Tiếng Anh D. Môn toán và môn văn
Câu 2: Kết quả của phép tính: \(\dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{{23}} - \dfrac{1}{6}\)
A. \(\dfrac{1}{{23}}\) B. \(\dfrac{{26}}{{69}}\) C. \(\dfrac{3}{{23}}\) D. \(\dfrac{2}{{23}}\)
Câu 3: Kết quả của phép tính: \({2^{23}}:{4^3}\) là:
A. \({2^{17}}\) B. \({2^{26}}\) C. \({2^{29}}\) D. \({2^{20}}\)
Câu 4: Diện tích xung quanh của hình lập phương biết độ dài một bằng \(3a\).
A. \(9{a^2}\) B. \(27{a^2}\) C. \(32{a^2}\) D. \(36{a^2}\)
Câu 5: Cho \(\angle xBy = {60^0}\). Vẽ góc đối đỉnh với \(\angle xBy\). Hỏi góc này có số đo bằng bao nhiêu độ?
A. \({30^0}\) B. \({60^0}\) C. \({90^0}\) D. \({120^0}\)
Câu 6: Tính thể tích hộp sữa có dạng hình hộp chữ nhật như hình vẽ bên dưới:

A. \(1000\,c{m^3}\) B. \(1500\,c{m^3}\)
C. \(1000\,c{m^2}\) D. \(1500\,c{m^2}\)
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm)
Thực hiện phép tính:
a) \(\dfrac{{ - 4}}{7} - \dfrac{5}{{13}}.\dfrac{{ - 39}}{{25}} + \dfrac{{ - 1}}{{42}}:\left( { - \dfrac{5}{6}} \right)\) b) \(\left( {\dfrac{4}{5} + \dfrac{{ - 9}}{7}} \right):\dfrac{{2025}}{{2030}} + \left( {\dfrac{{ - 5}}{7} - \dfrac{{ - 6}}{5}} \right):\dfrac{{2025}}{{2030}}\)
c) \({\left( {{3^2}} \right)^2} - {\left( { - {2^3}} \right)^2} - {\left( { - {5^2}} \right)^2}\) d) \({2^3} + 3.{\left( {\dfrac{1}{2}} \right)^0}.{\left( {\dfrac{1}{2}} \right)^2}.4 + \left[ {{{\left( { - 2} \right)}^2}:\dfrac{1}{2}} \right]:8\)
Bài 2: (1,0 điềm)
So sánh:
a) \(5\) và \(\sqrt {16} \) b) \(\sqrt {9.16} \) và \(\sqrt 9 .\sqrt {16} \).
c) \(\sqrt 7 + \sqrt {15} \) và \(7\) d) \(\sqrt {50} - \sqrt 2 \) và \(\sqrt {50 - 2} \)
Bài 3: (2,0 điểm) Tìm \(x\), biết:
a) \(\left( {2x + \dfrac{5}{3}} \right).\left( {\dfrac{5}{4} - x} \right) = 0\) b) \(\dfrac{3}{5}x + \left( {x + 0,5} \right) = \dfrac{{ - 13}}{{15}}\)
c) \({3^x} + {3^{x + 2}} = {9^{17}} + {27^{12}}\) d) \(\dfrac{1}{2}{.2^x} + {4.2^x} = {9.2^5}\)
Bài 4: (1,0 điểm)
Một chiếc hộp đựng đồ đa năng có dạng hình hộp chữ nhật với khung bằng thép, bên ngoài phủ vải và có kích thước như hình vẽ bên dưới:

a) Tính thể tích của hộp.
b) Người ta chọn vải có giá 15000 đồng cho \(0,5{m^2}\) vải. Hãy tính số tiền chi trả khi phủ bề ngoài của chiếc hộp.
Bài 5: (1,0 điểm)
Cho \(\angle xOy\). Vẽ \(\angle yOz\) kề bù với \(\angle xOy\). Vẽ \(\angle xOt\) kề bù với \(\angle xOy\). Vẽ \(On\) là tia phân giác \(\angle yOz\). Vẽ \(Om\) là phân giác của \(\angle xOt\). Khi đó \(\angle zOn\) và \(\angle xOm\) có phải là hai góc đối đỉnh hay không?
Đề 6
Phần trắc nghiệm ( 3 điểm)
Câu 1. Chọn khẳng định đúng
|
A. \(9 \notin Z\) |
B. \(\frac{{ - 1}}{3}\; \in Q\) |
|
C. \( - 5 \in I\) |
D. \(2,5\; \in Z\) |
Câu 2 . Số đối của \(\frac{{ - 8}}{9}\) là số nào?
|
A. \(\frac{9}{8}\). |
B. \(\frac{9}{{ - 8}}\). |
|
C. \( - \frac{8}{9}\). |
D. \(\frac{8}{9}\). |
Câu 3 . Hãy sắp xếp các số hữu tỉ sau theo thứ tự từ bé đến lớn: \(\,\frac{{ - 15}}{{ - 17}};\,0;\,\frac{{25}}{{17}}; - \frac{3}{{17}}\) ?
|
A. \( - \frac{3}{{17}};0;\,\frac{{25}}{{17}};\,\frac{{ - 15}}{{ - 17}}\). |
B. \(\frac{{25}}{{17}};\,0;\frac{{ - 15}}{{ - 17}};\, - \frac{3}{{17}}\). |
|
C. \( - \frac{3}{{17}};0;\,\frac{{ - 15}}{{ - 17}};\frac{{25}}{{17}}\). |
D. \(\frac{{25}}{{17}};\,\frac{{ - 15}}{{ - 17}};\,0;\, - \frac{3}{{17}}\). |
Câu 4 . Quan sát trục số sau. Khẳng định nào sau đây đúng?

|
A. Điểm \(A\) biểu diễn số hữu tỉ \(\frac{1}{2}\). |
B. Điểm \(B\) biểu diễn số hữu tỉ \(2\). |
|
C. Điểm \(C\) biểu diễn số hữu tỉ \(\frac{1}{2}\). |
D. Điểm A biểu diễn số hữu tỉ \(\frac{{ - 1}}{2}\). |
Câu 5 . Hình hộp chữ nhật có bao nhiêu cạnh?
|
A. 9 cạnh. |
B. 10 cạnh. |
|
C. 11 cạnh. |
D. 12 cạnh. |
Câu 6 . Ở mỗi đỉnh của hình lập phương có bao nhiêu góc?
|
A. 3 góc bẹt |
B. 3 góc vuông. |
|
C. Không có góc nào. |
D. 5 góc. |
Câu
7
.
Đường chéo của hình hộp chữ nhật \(ABCD.A'B'C'D'\) là đường nào?
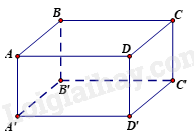
|
A. \(A'D\). |
B. \(BC'\). |
|
C. \(AC'\). |
D. \(BD\). |
Câu 8. Hình hộp chữ nhật \(ABCD.A'B'C'D'\)có \(BC = 7\,{\rm{cm}}\). Khẳng định nào sau đây sai ?
|
A. B’C’= 7 cm. |
B. \(AD = 7\,{\rm{cm}}\). |
|
C. \(A'D' = 7\,{\rm{cm}}\). |
D. \(E'B = 7\,{\rm{cm}}\). |
Câu 9. Trong các hình sau, hình nào là hình lăng trụ đứng tam giác
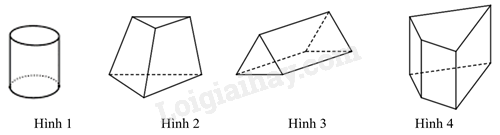
|
A. Hình 1. |
B. Hình 2. |
|
C. Hình 3. |
D. Hình 4 |
Câu 10. Cho hình lăng trụ đứng tứ giác \(MNPQ.EFGH\) có cạnh \(ME = 7\,{\rm{cm}}\),\(HG = 4\,{\rm{cm}}\). Khẳng định nào sau đây đúng?
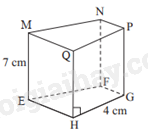
|
A. \(NF = 7\,{\rm{cm}}\). |
B. \(NF = 4\,{\rm{cm}}\). |
|
C. \(EH = 4\,{\rm{cm}}\). |
D. \(NP = 7\,{\rm{cm}}\). |
Câu
11.
Các mặt bên của hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ là những hình gì?
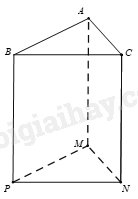
|
A. Tam giác. |
B. Tứ giác. |
|
C. Hình chữ nhật. |
D. Hình vuông. |
Câu 12. Cho hình lăng trụ đứng tam giác như hình bên. Mặt đáy của lăng trụ đứng là:
|
A. ABC. |
B. ABPM. |
|
C. ACMN. |
D. BCPN. |
Phần tự luận (7 điểm)
Bài 1 . (0,75 điểm). Trong các số 2,5; 0; \( - \frac{1}{3}\), \(1\frac{1}{2}\) số nào là số hữu tỉ dương? Vì sao?
Bài 2. (1,5 điểm). Thực hiện phép tính:
|
a. \(\frac{2}{3}:\frac{{ - 6}}{9} + \frac{1}{7}\); |
b. \(\frac{{ - 3}}{{11}} \cdot \frac{5}{9} + \frac{4}{9} \cdot \frac{{ - 3}}{{11}}\); |
c. \(\frac{{{9^5}{{.8}^2}}}{{{{27}^3}.16}}\); |
Bài 3 . (1,5 điểm). Tìm số hữu tỉ \(x\), biết:
|
a. \(25\% - x = 1\frac{5}{6}\); |
b. \(\frac{{ - 5}}{4} + \frac{2}{3}:x = 0,75\). |
Bài 4. (1,0 điểm). Cho hình hộp chữ nhật ABCD.MNHQ như hình vẽ, có AB = 5cm, BC = 7cm, AM = 3cm Tính diện tích xung quanh và thể tích của hình hộp chữ nhật này.
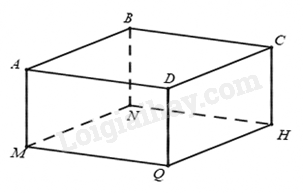
Bài 5. (0,75 điểm). Thùng đựng của một máy cắt cỏ có dạng lăng trụ đứng tam giác. Hãy tính thể tích của thùng.

Bài 6. (0,5 điểm). Một căn phòng hình hộp chữ nhật có chiều dài \(4,5m\), chiều rộng \(4m\) , chiều cao \(3m\) . Người ta muốn lăn sơn trần nhà và bốn bức tường. Biết rằng tổng diện tích các cửa là \(11\,{m^2}\). Tính diện tích cần lăn sơn ?
Bài 7. (1,0 điểm). Một cửa hàng bán quần áo có chương trình khuyến mãi như sau: Khách hàng có thẻ thành viên sẽ được giảm 15% tổng số tiền của hóa đơn. Bạn Bình có thẻ thành viên, bạn mua hai chiếc áo sơ mi, mỗi áo đều có giá 200 000 đồng và một quần Jeans với giá 350 000 đồng. Bạn đưa cho người thu ngân 1 triệu đồng. Hỏi bạn Bình được trả lại bao nhiêu tiền?
-------- Hết --------
Đề 7
Phần trắc nghiệm ( 3 điểm)
Câu 1. Tập hợp các số hữu tỉ kí hiệu là:
|
A. N. |
B. \({N*}\). |
|
C. Q . |
D. Z . |
Câu 2 . Số đối cùa \(\frac{{ - 2}}{3}\) là:
|
A. \(\frac{2}{3}\). |
B. \(\frac{3}{2}\). |
|
C. \(\frac{{ - 3}}{2}\). |
D. \(\frac{2}{{ - 3}}\). |
Câu 3 . Giá trị của \({\left( {{x^m}} \right)^n}\) bằng:
|
A. \({x^{m + n}}\). |
B. \({x^{m.n}}\). |
|
C. \({x^{m:n}}\) . |
D. \({x^m}^{ - n}\). |
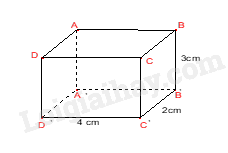
Câu 4 . Số mặt của hình hộp chữ nhật \(ABCD.A'B'C'D'\) là:
|
A. 3. |
B. 4. |
|
C. 5. |
D. 6. |
Câu 5 . Thể tích của hình hộp chữ nhật bên là:
|
A. 6. |
B. 8. |
|
C. 12. |
D. 24. |
Câu
6
.
Cho hình lăng trụ đứng tam giác \(ABC.A'B'C'\) các mặt bên của hình trên là những hình gì?
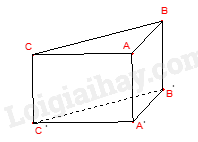
|
A. Tam giác. |
B. Tứ giác. |
|
C. Hình chữ nhật. |
D. Hình vuông. |
Câu 7 . Số đỉnh của hình hộp chữ nhật là:
|
A. 6. |
B. 8. |
|
C. 10. |
D. 12. |
Câu 8. Cho một hình lăng trụ đứng có diện tích đáy là S, chiều cao là h. Hỏi công thức tính thể tích của hình lăng trụ đứng là gì?
|
A. V = S.h. |
B. V = \(\frac{1}{2}S.h\). |
|
C. V = 2S.h. |
D. V = 3S.h. |
Câu 9. Hai đường thẳng xx’ và yy’ cắt nhau tại O. Góc đối đỉnh của góc \(\widehat {xOy}'\) là:
|
A. \(\widehat {x'Oy}'\). |
B. \(\widehat {x'Oy}\). |
|
C. \(\widehat {xOy}\). |
D. \(\widehat {y'Ox}\). |
Câu 10.
Cho hình vẽ, biết \(\widehat {xOy} = {40^0}\), Oy là tia phân giác của góc \(\widehat {xOz}\). Khi đó số đo \(\widehat {yOz}\) bằng:
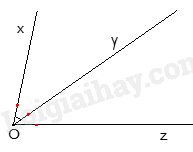
|
A. 20 0 . |
B. 140 0 . |
|
C. 80 0 . |
D. 40 0 . |
Câu 11. Kết quả của phép tính \({2^2}{.2^5}\) là:
|
A. 2 10 . |
B. 2 3 . |
|
C. 2 5 . |
D. 2 7 . |
Câu 12. Kết quả của phép tính \(\frac{{ - 3}}{{20}} + \frac{{ - 2}}{{15}}\) là:
|
A. \(\frac{{ - 1}}{{35}}\). |
B. \(\frac{{ - 17}}{{60}}\). |
|
C. \(\frac{{ - 5}}{{35}}\). |
D. \(\frac{{ - 1}}{{60}}\). |
Phần tự luận (7 điểm)
Bài 1 . (1,75 điểm). Tính:
|
a. \(\frac{7}{6} - \frac{1}{6}:\frac{2}{3}\); |
b.\(13,3\,.\,4,5\; - \;44\,.\,13,3\); |
c. \(2021 - {\left( {\frac{1}{3}} \right)^2}{.3^2}\). |
Bài 2. (1,0 điểm). Tìm x biết:
|
a. \(2x - \frac{1}{3} = \frac{5}{3}\); |
b. \({\left( {2x + 3} \right)^2} = 25\); |
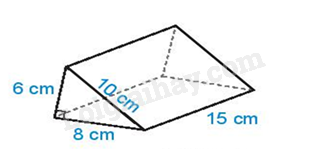
Bài 3 . (1,5 điểm). Tính diện tích xung quanh và thể tích hình lăng trụ đứng trong hình sau:
Bài 4. (1,25 điểm). Một ngôi nhà có cấu trúc và kích thước như hình sau. Tính thể tích phần không gian được giới hạn bởi ngôi nhà đó.

Bài 5. ( 1 điểm). Cho đường thẳng aa’ cắt bb’ tại O.
a. Kể tên các cặp góc đối đỉnh
b. Kể tên các cặp góc kề bù
c. Dùng dụng cụ học tập để vẽ tia phân giác của góc aOb.
-------- Hết --------
Đề 8
Phần trắc nghiệm ( 3 điểm)
Câu 1. Chọn khẳng định đúng
|
A. \(\frac{3}{2} \in \mathbb{Q}.\) |
B. \(\frac{3}{2} \in \mathbb{Z}\). |
|
C. \(\frac{{ - 9}}{5} \notin \mathbb{Q}\). |
D. \( - 6 \in \mathbb{N}\). |
Câu 2 . Số hữu tỉ dương là
|
A. \(\frac{{ - 11}}{3}.\) |
B. \( - \frac{{12}}{5}.\) |
|
C. \(\frac{{ - 5}}{{ - 7}}.\) |
D. \(\frac{{15}}{{ - 13}}.\) |
Câu 3 . Kết quả phép tính \(\frac{3}{7} + \frac{4}{7}.\frac{{ - 21}}{{35}}\) là
|
A. \(\frac{3}{{35}}\). |
B. \(\frac{{ - 21}}{{35}}\). |
|
C. \(\frac{{ - 11}}{{35}}\). |
D. \(\frac{{11}}{{35}}\). |
Câu 4 . Giá trị của \(x\) trong phép tính \(\frac{2}{5} - x = \frac{1}{3}\) bằng
|
A. \(\frac{7}{{30}}.\) |
B. \(\frac{{ - 1}}{{15}}.\) |
|
C. \(\frac{{11}}{{15}}.\) |
D. \(\frac{1}{{15}}.\) |
Câu 5 . Căn bậc hai số học của 81 là
|
A. 9 và -9 |
B. \(\frac{{ - 1}}{{81}}.\) |
|
C. \( - 9.\) |
D. \(9.\) |
Câu 6 . Khẳng định đúng là
|
A. \(\left| { - 3,5} \right| = - 3,5\) |
B. \(\left| { - 3,5} \right| = 3,5.\) |
|
C. \(\left| { - 3,5} \right| = \pm 3,5\) |
D. \(\left| { - 3,5} \right| > 3,5.\) |
Câu 7 . Số nào trong các số dưới đây viết được dưới dạng số thập phân hữu hạn
|
A. \(\frac{{ - 7}}{{15}}\). |
B. \(\frac{{ - 7}}{{24}}\). |
|
C. \(\frac{{ - 5}}{{32}}\). |
D. \(\frac{{12}}{{45}}\). |
Câu 8. Giá trị của x trong đẳng thức - 0,6 = 1,4 là
|
A. 2 hoặc -2. |
B. 0,6 hoặc -0,6. |
|
C. 2. |
D. -2. |
Câu 9. Giá trị của đẳng thức\(\sqrt {2 + 3 + 4 + 3 + 4} \)
|
A. 16. |
B. -16. |
|
C. 4. |
D. -4. |
Câu 10. Những đồ vật sau có dạng hình gì?

|
A. Hình hộp chữ nhật |
B. Hình vuông |
|
C. Hình lập phương |
D. Hình chữ nhật |
Câu 11. Cho hình hộp chữ nhật có kích thước như hình vẽ.
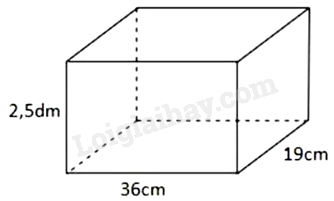
Diện tích xung quanh của hình hộp chữ nhật là:
|
A. \(2750{\rm{c}}{{\rm{m}}^2}\) |
B. \(275{\rm{c}}{{\rm{m}}^2}\) |
|
C. \(2770{\rm{c}}{{\rm{m}}^2}\) |
D. \(27{\rm{c}}{{\rm{m}}^2}\) |
Câu 12. Cho hình bên dưới, biết số đo \(\widehat {xHy} = {38^0}\). Số đo \(\widehat {{\rm{yHm}}} = \) ?
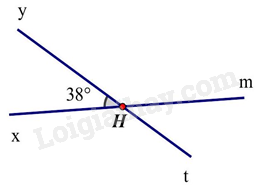
|
A. \({38^0}\) |
B. \({142^0}\) |
|
C. \({52^0}\) |
D. \({128^0}\) |
PHẦN II. TỰ LUẬN (7 điểm)
Bài 1 . ( 2,0 điểm)
1. So sánh: - 3,7634 và – 3,7654.
2. Thực hiện các phép tính sau
|
a. \(\frac{2}{9} - {\left( {\frac{1}{2}} \right)^2} + \frac{5}{{18}}\) |
b. \(17\frac{1}{3}.\left( {\frac{{ - 5}}{7}} \right) - 10\frac{1}{3}.\left( {\frac{{ - 5}}{7}} \right)\) |
Bài 2. ( 1,5 điểm) Tìm x, biết
|
a. x + 4,5 = 7,5 |
b. \(\frac{2}{3}.x + \frac{1}{2} = \frac{4}{9}\) |
c. |x| - 0,7 = 1,3 |
Bài 3 . (2,5 điểm)
1. Cho một căn phòng có dạng hình hộp chữ nhật. Biết chiều dài, chiều rộng căn phòng lần lượt là 3m và 2m và chiều cao của căn phòng là 4m. a. Tính diện tích mặt sàn căn phòng. b. Để sơn xung quanh căn phòng cần trả bao nhiêu tiền công cho thợ sơn biết giá công sơn là 50 000 đồng cho mỗi m 2 .
2. Cho hình vẽ bên. Biết hai đường thẳng a và b song song với nhau và \(\widehat {{A_1}} = {70^0}\).
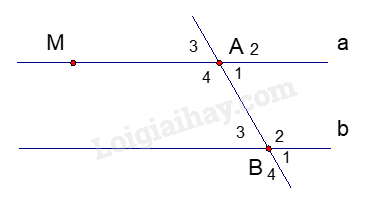
a. Tính số đo của \(\widehat {{A_3}};\,\widehat {{B_3}}\)
b. Kẻ đường thẳng c vuông góc với đường thẳng a tại M.
Chứng tỏ rằng: c \( \bot \) b
Bài 4. ( 1,0 điểm). So sánh A và B biết:
\(A = \frac{{{{2023}^{2023}} + 1}}{{{{2023}^{2024}} + 1}}\) và \(B = \frac{{{{2023}^{2022}} + 1}}{{{{2023}^{2023}} + 1}}\)
-------- Hết --------
Đề 9
Phần trắc nghiệm ( 3 điểm)
Câu 1: Số đối của số hữu tỉ \( - 0,25\) là
|
A. \( - 0,25.\) |
B. \(\frac{{ - 1}}{4}.\) |
|
C. \( - 4.\) |
D. \(0,25.\) |
Câu 2: Trong các số sau, số nào là số hữu tỉ âm?
|
A. \(\frac{0}{{ - 2}}\) |
B. \(\frac{{ - 2}}{{ - 1}}\) |
|
C. \( - \frac{1}{2}\) |
D. \(\frac{{ - \left( { - 2} \right)}}{3}\) |
Câu 3: Khi biểu diễu số hữu tỉ a và b trên trục số nằm ngang ta thấy điểm a nằm bên phải điểm b thì
|
A. \(a < b.\) |
B. \(a > b.\) |
|
C. \(a = b.\) |
D. \(a = - b.\) |
Câu 4: Kết quả của phép tính \({7^{10}}:7\) viết dưới dạng lũy thừa là
|
A. \({7^9}.\) |
B. \({7^{11}}.\) |
|
C. \({7^{10}}.\) |
D. \({1^{10}}.\) |
Câu 5: Với \(a,b,c\)là ba số hữu tỉ bất kì, nếu \(a - b = c\) thì
|
A. \(a = b + c.\) |
B. \(a = - b + c.\) |
|
C. \(a = b - c.\) |
D. \(a = - b - c.\) |
Câu 6: Với \(x,y,z\)là ba số hữu tỉ bất kì, sau khi bỏ ngoặc ta được \(x - \left( {y + z} \right)\) bằng
|
A. \(x - y + z.\) |
B. \(x - y - z.\) |
|
C. \(x + y - z.\) |
D. \(x + y + z.\) |
Câu 7: Những đồ vật sau có dạng hình gì?

|
A. Hình hộp chữ nhật |
B. Hình vuông |
|
C. Hình lập phương |
D. Hình chữ nhật |
Câu 8: Cho hình lập phương \(ABCD.MNPQ\) có độ dài cạnh là \(2{\rm{\;cm}}\). Tính tổng diện tích các mặt của hình lập phương.
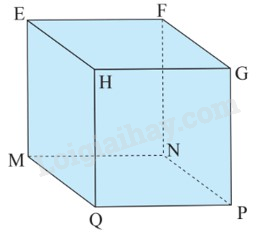
|
A. \(8{\rm{\;c}}{{\rm{m}}^2}\). |
B. \(12{\rm{\;c}}{{\rm{m}}^2}\). |
|
C. \(24{\rm{\;c}}{{\rm{m}}^2}\). |
D. \(20{\rm{\;c}}{{\rm{m}}^2}\). |
Câu 9: Chọn phát biểu đúng trong các phát biểu sau: A. Hình lăng trụ tam giác có 4 mặt, 6 đỉnh; B. Hình lăng trụ tam giác có 5 mặt, 6 đỉnh;
C. Hình lăng trụ tam giác có 6 mặt, 5 đỉnh;
D. Hình lăng trụ tam giác có 4 mặt, 4 đỉnh.
Câu 10: Quan sát hình lập phương EFGH.MNPQ, biết \({\rm{MN}} = 3{\rm{\;cm}}\), độ dài các cạnh \({\rm{EF}},{\rm{NF}}\) bằng bao nhiêu?
|
A. \({\rm{EF}} = {\rm{NF}} = 3{\rm{\;cm}}\) |
B. \({\rm{EF}} = 3{\rm{\;cm}},{\rm{NF}} = 6{\rm{\;cm}}\) |
|
C. \({\rm{EF}} = {\rm{NF}} = 6{\rm{\;cm}}\) |
D. Các đáp án đều sai |
Câu 11 : Cho hình lăng trụ đứng tam giác có kích thước như hình vẽ.
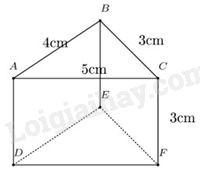
Diện tích xung quanh của hình lăng trụ đứng trên là:
|
A. 36cm 2 . |
B. 30cm 2 . |
|
C. 36cm 3 . |
D. 30cm 3 . |
Câu 12: Cho các khẳng định sau: (I). Hai góc đối đỉnh thì bằng nhau. (II). Hai góc bằng nhau thì đối đỉnh. (III). Hai góc kề bù là hai góc vừa kề nhau, vừa bù nhau.
Số khẳng định đúng là:
|
A. 1. |
B. 2. |
|
C. 3. |
D. 0. |
Phần tự luận (7 điểm)
Bài 1 : (0,5 điểm) So sánh hai số hữu tỉ sau: \(0,25\) và \(\frac{1}{3}\)
Bài 2 : (2,0 điểm) Thực hiện phép tính:
|
a) \(\left( { - 0,25} \right).40\; + 3\) |
b) \(\frac{1}{7} \cdot \frac{{ - 3}}{8} + \frac{{ - 13}}{8} \cdot \frac{1}{7}\) |
|
c) \(\left[ {\left( {\frac{2}{3} - \frac{1}{4}} \right) + {{\left( { - 2} \right)}^2}.3} \right] - 1\) |
Bài 3: (2,0 điểm) Tìm x, biết:
|
a) \(x - 4 = \frac{1}{2}\) |
b) \(2.\left( {x - 1} \right) = {3^3} - 1\) |
Bài 4 : (1,5 điểm) Một nhà kho có dạng hình lăng trụ đứng, đáy là hình thang vuông. Chiều cao của hình lăng trụ đứng (là chiều dài của nhà kho) bằng \(6{\rm{\;m}}\). Đường cao của đáy (là chiều rộng của nhà kho) bằng \(5{\rm{\;m}}\). Các cạnh đáy của hình thang vuông dài \(3{\rm{\;m}}\) và \(4{\rm{\;m}}\). Tính thể tích của nhà kho.
Bài 5 : (1,0 điểm) Một phòng học hình hộp chữ nhật có chiều dài \(8{\rm{\;m}}\), chiều rộng \(5{\rm{\;m}}\), chiều cao \(4{\rm{\;m}}\). Người ta quét vôi bên trong lớp học, kể cả trần. Biết tổng diện tích các cửa ra vào và cửa sổ là \(10{\rm{\;}}{{\rm{m}}^2}\). Tính diện tích phải quét vôi.
-------- Hết --------
Đề 10
Phần trắc nghiệm ( 3 điểm)
Câu 1: Chọn đáp án đúng
|
A. \( - 7 \in \mathbb{N}\) |
B. \( - 7 \notin \mathbb{Z}\) |
|
C. \( - 7 \notin \mathbb{Q}\) |
D. \(\frac{1}{2} \in \mathbb{Q}\) |
Câu 2: Kết quả của phép tính: \(\frac{{ - 3}}{{20}} + \frac{{ - 2}}{{15}}\) là
|
A. \(\frac{{ - 1}}{{60}}\) |
B. \(\frac{{ - 17}}{{60}}\) |
|
C. \(\frac{{ - 5}}{{35}}\) |
D. \(\frac{1}{{60}}\) |
Câu 3: Kết quả của phép tính: - 0,35. \(\frac{2}{7}\) là
|
A. - 0,1 |
B. -1 |
|
C. -10 |
D. -100 |
Câu 4: Kết quả của phép tính: \(\frac{{ - 26}}{{15}}:2\frac{3}{5}\) là
|
A. -6 |
B. \(\frac{{ - 3}}{2}\) |
|
C. \(\frac{{ - 2}}{3}\) |
D. \(\frac{{ - 3}}{4}\) |
Câu 5: Kết quả phép tính: \(\frac{3}{4} + \frac{1}{4}.\frac{{ - 12}}{{20}}\) là
|
A. \(\frac{{ - 12}}{{20}}\) |
B. \(\frac{3}{5}\) |
|
C. \(\frac{{ - 3}}{5}\) |
D. \(\frac{{ - 9}}{{84}}\) |
Câu 6: Giá trị của biểu thức : | - 3,4 | : | +1,7 | - 0,2 là
|
A. - 1,8 |
B. 1,8 |
|
C. 0 |
D. - 2,2 |
Câu 7: Kết quả phép tính: \({\left( { - \frac{1}{3}} \right)^4}\)
|
A. \(\frac{1}{{81}}\). |
B. \(\frac{4}{{81}}\). |
|
C. \(\frac{{ - 1}}{{81}}\). |
D. \(\frac{{ - 4}}{{81}}\). |
Câu 8: Trong hình dưới đây có bao nhiêu hình lập phương, bao nhiêu hình hộp chữ nhật?

A. 2 hình lập phương, 3 hình hộp chữ nhật; B. 1 hình lập phương, 3 hình hộp chữ nhật; C. 2 hình lập phương, 2 hình hộp chữ nhật; D. 0 hình lập phương, 4 hình hộp chữ nhật.
Câu 9: Hãy chọn khẳng định sai. Hình lập phương ABCD.A'B'C'D' có:
|
A. 8 đỉnh |
B. 4 mặt bên |
|
C. 6 cạnh |
D. 6 mặt |
Câu 10: Cho hình hộp chữ nhật ABCD. EFGH. Cho AB = 4 cm, BC = 2 cm, AE = 4 cm. Khẳng định đúng là:
A. HG = 4 cm, HE = 2 cm, GC = 4 cm; B. HG = 2 cm, HE = 2 cm, GC = 4 cm; C. HG = 4 cm, HE = 2 cm, GC = 2 cm; D. HG = 4 cm, HE = 4 cm, GC = 4 cm.
Câu 11 : Tấm bìa bên dưới có thể tạo lập thành một hình lăng trụ đứng có đáy là tam giác đều.
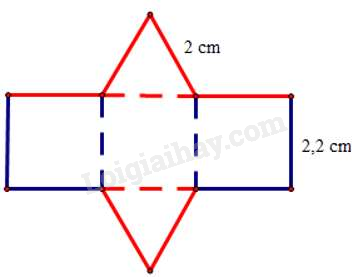
Chiều cao của hình lăng trụ đứng là:
|
A. 2 cm |
B. 2,2 cm |
|
C. 4 cm |
D. 4,4 cm |
Câu 12: Chọn phát biểu sai: A. Hai góc đối đỉnh thì bằng nhau; B. Hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia được gọi là hai góc đối đỉnh; C. Hai đường thẳng cắt nhau tại một điểm tạo thành hai cặp góc đối đỉnh; D. Hai góc bằng nhau thì đối đỉnh.
Phần tự luận (7 điểm)
Bài 1 : ( 1 điểm) Tìm x, biết
|
a. \(x - \frac{3}{4} = \frac{5}{{ - 7}}\) |
b. 100 - \(\left| {x + 1} \right| = 90\); |
Bài 2. (1,5 điểm) Thực hiện phép tính:
|
a) \(\frac{2}{3}:\frac{{ - 6}}{9} + \frac{1}{7}\); |
b) \(\frac{{ - 3}}{{11}} \cdot \frac{5}{9} + \frac{4}{9} \cdot \frac{{ - 3}}{{11}}\); |
c) \(\frac{{{9^5}{{.8}^2}}}{{{{27}^3}.16}}\). |
Bài 3. ( 1 điểm) Bác Long có một căn phòng hình hộp chữ nhật có một cửa ra vào và một cửa sổ hình vuông với các kích thước như hình vẽ.
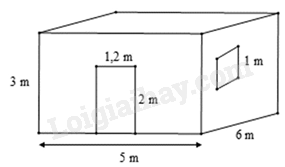
Hỏi bác Long cần trả bao nhiêu chi phí để sơn bốn bức tường xung quanh của căn phòng này (không sơn cửa)? Biết rằng để sơn mỗi mét vuông tốn 30 nghìn đồng.
Bài 4. (1,5 điểm) Một khối gỗ có dạng hình lăng trụ đứng đáy là tam giác vuông có kích thước thước hai cạnh góc vuông là 3 dm; 4 dm, cạnh huyền (cạnh đối diện với góc vuông) là 0,5 m. Người ta khoét một lỗ lăng trụ đứng đáy tam giác vuông hai cạnh góc vuông có kích thước là 1,5 dm; 2 dm; cạnh huyền 2,5 dm. Biết khối gỗ dài 0,45 m (hình vẽ).
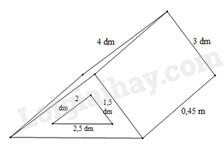
a) Tính thể tích của khối gỗ. b) Người ta muốn sơn tất cả các bề mặt của khối gỗ. Tính diện tích cần sơn (đơn vị mét vuông).
Bài 5. (1,5 điểm) Cho hình vẽ dưới đây:
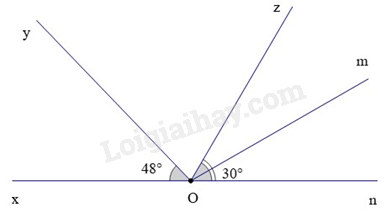 Biết rằng \(\widehat {xOy} = {48^0},\widehat {mOn} = {30^0}\) và Om là phân giác của \(\widehat {zOn}\).
a) Kể tên các góc (khác góc bẹt) kề với \(\widehat {zOm}\); góc kề bù với \(\widehat {mOn}\)
.
b) Tính số đo của góc \(\widehat {yOz}\).
Biết rằng \(\widehat {xOy} = {48^0},\widehat {mOn} = {30^0}\) và Om là phân giác của \(\widehat {zOn}\).
a) Kể tên các góc (khác góc bẹt) kề với \(\widehat {zOm}\); góc kề bù với \(\widehat {mOn}\)
.
b) Tính số đo của góc \(\widehat {yOz}\).
Bài 6. (0,5 điểm) Tìm hai số x, y. Tính giá trị nhỏ nhất của biểu thức: \({\rm{M}} = {({\rm{x}} - 5)^2} + 7\)
-------- Hết --------