Trong hình dưới đây, các tam giác nào đồng dạng với nhau

Đề bài

Trong hình dưới đây, các tam giác nào đồng dạng với nhau là

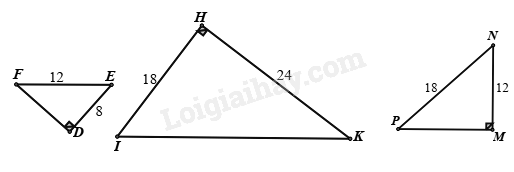
A.
$\Delta DEF\backsim \Delta HIK$ .
B.
$\Delta DEF\backsim \Delta MNP$ .
C.
$\Delta HIK\backsim \Delta MNP$ .
D.
Cả 3 tam giác đồng dạng.

Phương pháp giải

Dựa vào các trường hợp đồng dạng của hai tam giác vuông.

Xét $\Delta DEF$ và $\Delta MNP$ có:

$\begin{array}{l}\widehat D = \widehat M = {90^0}\\\frac{{DE}}{{MN}} = \frac{{EF}}{{NP}}\left( {\frac{8}{{12}} = \frac{{12}}{{18}}\left( { = \frac{2}{3}} \right)} \right)\end{array}$

nên $\Delta DEF\backsim \Delta MNP$ (cạnh huyền – cạnh góc vuông)

Áp dụng định lí Pythagore vào tam giác HIK có:

$KI = \sqrt {{{18}^2} + {{24}^2}} = 30$

Vì $\frac{8}{{12}} = \frac{2}{3} \ne \frac{{18}}{{30}} = \frac{3}{5}$ nên $\Delta DEF$ không đồng dạng với $\Delta HIK$ .

Điều này dẫn đến $\Delta MNP$ không đồng dạng với $\Delta HIK$ (vì $\Delta DEF\backsim \Delta MNP$ )

Đáp án B.

Đáp án : B