Đề bài
Con hãy điền từ / cụm từ/ số thích hợp vào các ô trống
Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A’B’C’D’. Biết A(2;4;0), B(4;0;0), C(-1;4;-7) và D’(6;8;10). Tổng hoành độ, tung độ, cao độ của điểm B’ bằng bao nhiêu?
Đáp án:
Đáp án
Đáp án:
Phương pháp giải
Tìm giao điểm O của AC và BD, từ đó tìm được D. Thông qua →BB′=→DD′ ta tìm được tọa độ B’.
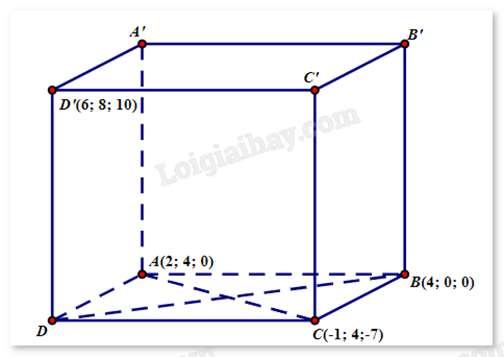
Giả sử D(a;b;c), B’(a’;b’;c’). Gọi O là giao điểm của AC và BD, suy ra O là trung điểm của AC.
Từ đó, ta tính được tọa độ điểm O(12;4;−72).
Vì O là trung điểm của BD nên từ B(4;0;0) ta tìm được D(-3;8;-7).
Vậy, →DD′=(9;0;17). Mà ABCD.A’B’C’D’ là hình hộp nên →BB′=→DD′=(9;0;17).
Mà →BB′=(a′−4;b′;c′), suy ra a’ = 13, b’ = 0, c’ = 17.
Vậy B’(13;0;17). Tổng hoành độ, tung độ, cao độ của điểm B’ bằng 13 + 0 + 17 = 30.