Trong mặt phẳng (P), cho hình bình hành ABCD tâm O, ngoài mặt phẳng (P) cho một điểm S.
a) C là một điểm chung của hai mặt phẳng (SAB) và (SCD)
b) Giao tuyến của hai mặt phẳng (SCB) và (SCD) là đường thẳng SC
c) Đường thẳng AB song song với mặt phẳng (SCD)
d) Giao điểm của đường thẳng BC với mặt phẳng (SBD) là điểm C
a) C là một điểm chung của hai mặt phẳng (SAB) và (SCD)
b) Giao tuyến của hai mặt phẳng (SCB) và (SCD) là đường thẳng SC
c) Đường thẳng AB song song với mặt phẳng (SCD)
d) Giao điểm của đường thẳng BC với mặt phẳng (SBD) là điểm C
Sử dụng các định lý về đường thẳng song song với mặt phẳng, cách tìm giao tuyến của hai mặt phẳng.
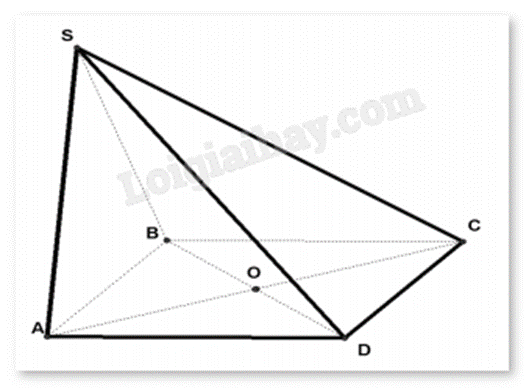
a) Sai . C không thuộc mặt phẳng (SAB).
b) Đúng . Giao tuyến của hai mặt phẳng (SCB) và (SCD) là đường thẳng SC.
c) Đúng . Vì ABCD là hình bình hành nên AB//CD, khi đó AB//(SCD).
d) Sai . Giao điểm của đường thẳng BC với mặt phẳng (SBD) là điểm B.