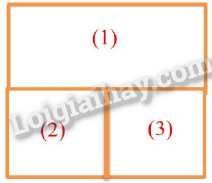
Trong một bình cao có tiết diện thắng là hình vuông, được chia làm ba ngăn như hình vẽ. Hai ngăn nhỏ có tiết diện thẳng cũng là một hình vuông có cạnh bằng nửa cạnh của bình. Đổ chất lỏng vào các ngăn đến cùng một độ cao: ngăn thứ nhất là chất lỏng ở nhiệt độ t \({t_1}\) \( = {65^ \circ }{\rm{C}}\), ngăn 2 là chất lỏng ở nhiệt độ \({{\rm{t}}_2} = {35^ \circ }{\rm{C}}\), ngăn 3 là chất lỏng ở nhiệt độ \({{\rm{t}}_3}\) \( = {20^ \circ }{\rm{C}}\). Biết rằng thành bình cách nhiệt rất tốt, nhưng các vách ngăn có dẫn nhiệt không tốt lắm, nhiệt lượng truyền qua các vách ngăn trong một đơn vị thời gian tỉ lệ với diện tích tiếp xúc của chất lỏng và với hiệu nhiệt độ ở hai bên vách ngăn.
Xem rằng về phương diện nhiệt thì cả ba chất lỏng nói trên là giống nhau. Bỏ qua sự trao đổi nhiệt với bình và với môi trường. Sau một thời gian thì nhiệt độ ngăn thứ nhất giảm \({\rm{\Delta }}{t_1} = {1^ \circ }{\rm{C}}\). Ở ngăn thứ ba, nhiệt độ biến đổi bao nhiêu trong thời gian trên?
Vận dụng lí thuyết cân bằng nhiệt
Diện tích tiếp xúc của từng cặp chất lỏng trong bài toàn là như nhau
Vậy nhiệt lượng truyền qua giữa chúng tỉ lệ với hiệu nhiệt độ với cùng một hệ số tỉ lệ là k
Ngăn 1 tỏa nhiệt sang ngăn 2 là \({{\rm{Q}}_{12}} = {\rm{k}}\left( {{{\rm{t}}_1} - {{\rm{t}}_2}} \right)\)
Ngăn 1 tỏa nhiệt sang ngăn 3 là \({Q_{13}} = k\left( {{t_1} - {t_3}} \right)\)
Ngăn 2 tỏa nhiệt sang ngăn 3 là \({{\rm{Q}}_{23}} = {\rm{k}}\left( {{{\rm{t}}_2} - {{\rm{t}}_3}} \right)\)
Phương trình cân bằng nhiệt:
Ngăn 1 có \({{\rm{Q}}_{12}} + {{\rm{Q}}_{13}} = 2{\rm{mc\Delta }}{{\rm{t}}_1} \Rightarrow {\rm{k}}\left( {2{{\rm{t}}_1} - {{\rm{t}}_2} - {{\rm{t}}_3}} \right) = 2{\rm{mc\Delta }}{{\rm{t}}_1}\)
Ngăn 2 có \({{\rm{Q}}_{12}} - {{\rm{Q}}_{23}} = {\rm{mc\Delta }}{{\rm{t}}_2} \Rightarrow {\rm{k}}\left( {{{\rm{t}}_1} - 2{{\rm{t}}_2} + {{\rm{t}}_3}} \right) = {\rm{mc\Delta }}{{\rm{t}}_2}\)
Ngăn 3 có \({{\rm{Q}}_{13}} + {{\rm{Q}}_{23}} = {\rm{mc\Delta }}{{\rm{t}}_3} \Rightarrow {\rm{k}}\left( {{{\rm{t}}_1} + {{\rm{t}}_2} - 2{{\rm{t}}_3}} \right) = {\rm{mc\Delta }}{{\rm{t}}_3}\)
\( \Rightarrow \frac{{2{{\rm{t}}_1} - {{\rm{t}}_2} - {{\rm{t}}_3}}}{{2{\rm{\Delta }}{{\rm{t}}_1}}} = \frac{{{{\rm{t}}_1} - 2{{\rm{t}}_2} + {{\rm{t}}_3}}}{{{\rm{\Delta }}{{\rm{t}}_2}}} = \frac{{{{\rm{t}}_1} + {{\rm{t}}_2} - 2{{\rm{t}}_3}}}{{{\rm{\Delta }}{{\rm{t}}_3}}}\)
\( \Rightarrow \frac{{2.65 - 35 - 20}}{{2.1}} = \frac{{65 - 2.35 + 20}}{{{\rm{\Delta }}{t_2}}} = \frac{{65 + 35 - 2.20}}{{{\rm{\Delta }}{t_3}}}\)
\( \Rightarrow {\rm{\Delta }}{{\rm{t}}_2} = 0,{4^ \circ }{\rm{C}}\) và \({\rm{\Delta }}{{\rm{t}}_3} = 1,{6^ \circ }{\rm{C}}\).
Đáp án: 1,6