Trong một cuộc thi gói bánh vào dịp năm mới, mỗi đội chơi được sử dụng tối đa 20 kg gạo nếp, 2 kg thịt ba chỉ, 5 kg đậu xanh để gói bánh chưng và bánh tét. Để gói một cái bánh chưng cần 0,4 kg gạo nếp, 0,05 kg thịt và 0,1 kg đậu xanh. Để gói một cái bánh tét cần 0,6 kg gạo nếp, 0,075 kg thịt và 0,15 kg đậu xanh. Gọi số bánh chưng gói được là x, số bánh tét gói được là y.
a) Biểu thức biểu diễn số kg gạo nếp cần dùng là 0,4x + 0,6y.
b) Biểu thức biểu diễn số thịt ba chỉ cần dùng là 0,05x + 0,1y.
c) Cặp (x; y) thỏa mãn bài toán thuộc miền nghiệm của hệ \(\left\{ {\begin{array}{*{20}{c}}{2x + 3y \le 80}\\{x,y \ge 0}\end{array}} \right.\).
d) Mỗi cái bánh chưng nhận được 5 điểm thưởng, mỗi cái bánh tét nhận được 7 điểm thưởng. Để điểm thưởng lớn nhất thì gói 35 cái bánh chưng và 5 cái bánh tét.
a) Biểu thức biểu diễn số kg gạo nếp cần dùng là 0,4x + 0,6y.
b) Biểu thức biểu diễn số thịt ba chỉ cần dùng là 0,05x + 0,1y.
c) Cặp (x; y) thỏa mãn bài toán thuộc miền nghiệm của hệ \(\left\{ {\begin{array}{*{20}{c}}{2x + 3y \le 80}\\{x,y \ge 0}\end{array}} \right.\).
d) Mỗi cái bánh chưng nhận được 5 điểm thưởng, mỗi cái bánh tét nhận được 7 điểm thưởng. Để điểm thưởng lớn nhất thì gói 35 cái bánh chưng và 5 cái bánh tét.
Lập hệ bất phương trình.
a) Đúng. Biểu thức biểu diễn số kg gạo nếp cần dùng là 0,4x + 0,6y.
b) Sai. Biểu thức biểu diễn số thịt ba chỉ cần dùng là 0,05x + 0,075y.
c) Đúng. Với số bánh chưng gói được là x, số bánh tét gói được là y, ta có:
Số kg gạo nếp cần dùng là 0,4x + 0,6y.
Số thịt ba chỉ cần dùng là 0,05x + 0,075y.
Số đậu xanh cần dùng là 0,1x + 0,15y.
Theo giả thiết ta có \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{0,4x + 0,6y \le 20}\\{0,05x + 0,075y \le 2}\\{0,1x + 0,15y \le 5}\end{array}} \right.\) hay \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{2x + 3y \le 100}\\{2x + 3y \le 80}\\{2x + 34y \le 100}\end{array}} \right.\), rút gọn ta được \(\left\{ {\begin{array}{*{20}{c}}{x,y \ge 0}\\{2x + 3y \le 80}\end{array}} \right.\).
d) Sai. Vẽ miền nghiệm của hệ:
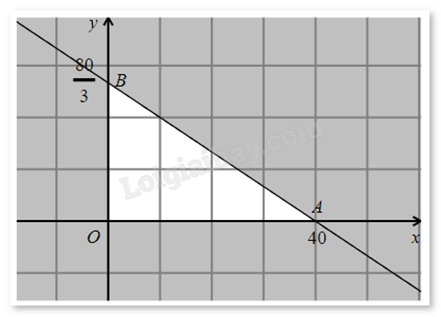
Ta thấy miền nghiệm của hệ là một miền tam giác OAB kể cả biên, trong đó O(0;0), A(40;0), \(B\left( {0;\frac{{80}}{3}} \right)\).
Số điểm thưởng nhận được là P = 5x + 7y.
P đạt giá trị lớn nhất tại một trong các đỉnh của tam giác. Thay tọa độ các điểm trên vào P, thấy P đạt giá trị lớn nhất bằng 200 tại A(40;0).
Vậy, cần gói 40 cái bánh chưng để điểm thưởng lớn nhất.