Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24g hương liệu, 9 lít nước và 210g đường để pha chế nước cam và nước táo.
Để pha chế 1 lít nước cam cần 30g đường, 1 lít nước và 1g hương liệu.
Để pha chế 1 lít nước táo cần 10g đường, 1 lít nước và 4g hương liệu.
Gọi x, y lần lượt là số lít nước cam, nước táo được tạo thành.
a) Biểu thức biểu diễn số gam đường cần dùng là 30x + 10y.
b) Biểu thức biểu diễn số gam hương liệu cần dùng là x + y.
Cặp (x; y) thỏa mãn bài toán thuộc miền nghiệm của hệ \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{3x + y \le 21}\\{x + y \le 9}\\{x + 4y \le 24}\end{array}} \right.\).
d) Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Để điểm thưởng lớn nhất thì cần pha chế 4 lít nước cam và 5 lít nước táo.
a) Biểu thức biểu diễn số gam đường cần dùng là 30x + 10y.
b) Biểu thức biểu diễn số gam hương liệu cần dùng là x + y.
Cặp (x; y) thỏa mãn bài toán thuộc miền nghiệm của hệ \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{3x + y \le 21}\\{x + y \le 9}\\{x + 4y \le 24}\end{array}} \right.\).
d) Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Để điểm thưởng lớn nhất thì cần pha chế 4 lít nước cam và 5 lít nước táo.
Lập hệ bất phương trình.
a) Đúng. Biểu thức biểu diễn số gam đường cần dùng là 30x + 10y.
b) Sai. Biểu thức biểu diễn số gam hương liệu cần dùng là x + 4y.
c) Đúng. Với x, y lần lượt là số lít nước cam, nước táo được tạo thành, ta có:
30x + 10y là số gam đường cần dùng.
x + y là số lít nước cần dùng.
x + 4y là số gam hương liệu cần dùng.
Theo giả thiết ta có \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{30x + 10y \le 210}\\{x + y \le 9}\\{x + 4y \le 24}\end{array}} \right.\) hay \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{3x + y \le 21}\\{x + y \le 9}\\{x + 4y \le 24}\end{array}} \right.\).
d) Đúng. Vẽ miền nghiệm của hệ:
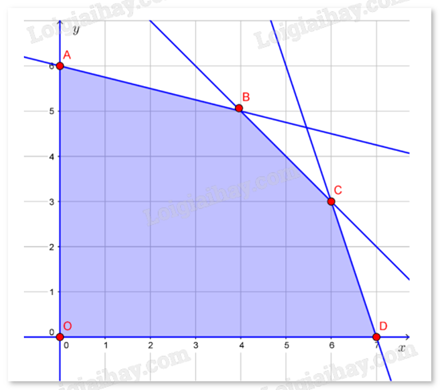
Ta thấy miền nghiệm của hệ là một miền ngũ giác OABCD kể cả biên, trong đó O(0;0), A(0;6), B(4;5), C(6;3) và D(7;0).
Số điểm thưởng nhận được là P = 60x + 80y.
P đạt giá trị lớn nhất tại một trong các đỉnh của ngũ giác. Thay tọa độ các điểm trên vào P, thấy P đạt giá trị lớn nhất bằng 640 tại B(4;5).
Vậy, cần pha chế 4 lít nước cam và 5 lít nước táo.