Tứ giác ABCD có AB = BC; CD = DA , góc B = 100 độ ; góc D = — Không quảng cáo

Phương pháp giải

Sử dụng tính chất của tam giác cân và tổng các góc trong tam giác bằng \({180^o}\)

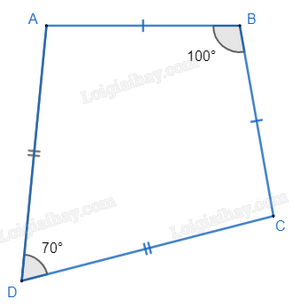
Xét tam giác ABC có AB = AC

\( \Rightarrow \Delta ABC\) cân tại B mà \(\widehat B = {100^o}\)

\( \Rightarrow \widehat {BAC} = \widehat {BCA} = \frac{{{{180}^o} - {{100}^o}}}{2} = {40^o}\)

Xét tam giác ADC có CD = DA

\( \Rightarrow \Delta A{{D}}C\) cân tại D có \(\widehat {A{{D}}C} = {70^o}\)

\( \Rightarrow \widehat {DAC} = \widehat {DCA} = \frac{{{{180}^o} - {{70}^o}}}{2} = {55^o}\)

Từ đó ta có:

\(\begin{array}{l}\widehat A = \widehat {BA{{D}}} = \widehat {BAC} + \widehat {CA{{D}}}\\ \Rightarrow \widehat A = \widehat {BA{{D}}} = {40^o} + {55^o} = {95^o}\end{array}\)

Và: \(\begin{array}{l}\widehat C = \widehat {BC{{D}}} = \widehat {BCA} + \widehat {AC{{D}}}\\ \Rightarrow \widehat C = \widehat {BC{{D}}} = {40^o} + {55^o} = {95^o}\end{array}\)

Vậy: \(\widehat A = \widehat C = {95^o}\)