Tứ giác ABCD có: Góc A + góc C = 60 độ Các tia phân giác — Không quảng cáo

Phương pháp giải

Áp dụng tính chất của tia phân giác và định lí tổng các góc trong tứ giác bằng ${360^o}$

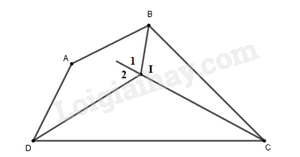
Xét tam giác BIC có:

$\widehat {IBC} = \widehat {{I_1}} - \widehat {BCI}$

Xét tam giác DIC có:

$\widehat {I{{D}}C} = \widehat {{I_2}} - \widehat {IC{{D}}}$

Nên: $\widehat {IBC} + \widehat {I{{D}}C} = \left( {\widehat {{I_1}} + \widehat {{I_2}}} \right) - \left( {\widehat {{C_1}} + \widehat {{C_2}}} \right) = \widehat {BI{{D}}} - \widehat C$

Tứ giác ABID:

$\widehat {ABI} + \widehat {A{{D}}I} = {360^o} - \widehat A - \widehat {BI{{D}}}$

Do: $\widehat {ADI} = \widehat {I{{D}}C}$ (tính chất của tia phân giác)

Nên: $\widehat {IBC} + \widehat {I{{D}}C} = \widehat {ABI} + \widehat {A{{D}}I}$

Hay

$\begin{array}{l}\widehat {BI{{D}}} - \widehat C = {360^o} - \widehat A - \widehat {BI{{D}}}\\ \Leftrightarrow 2\widehat {BI{{D}}} = {360^o} - \left( {\widehat A - \widehat C} \right) = {360^o} - {60^o} = {300^o}\end{array}$

Suy ra: $\widehat {BI{{D}}} = {150^o}$