Vẽ, cắt và gấp mảnh bìa như đã chỉ ra ở hình bên dưới để được hình chóp tứ giác đều.
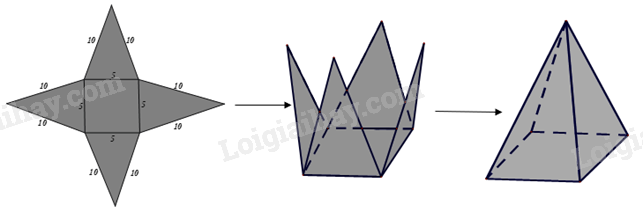
a) Trong hình vẽ trên có bao nhiêu tam giác cân bằng nhau?
b) Tính diện tích tất cả các mặt của hình chóp tứ giác đều này. Biết độ dài trung đoạn của hình chóp tứ giác đều là 9,68 cm.
a) Dựa vào đặc điểm của hình chóp tứ giác đều để xác định.
b) Tính diện tích xung quanh của hình chóp:
Cách 1: Sử dụng công thức \({S_{xq}} = \frac{1}{2}C.d\).
Cách 2: Sử dụng công thức \({S_{xq}} = 4.\)S mặt bên .
Tính mặt đáy.
a) Trong hình vẽ bên dưới có 4 tam giác cân bằng nhau.
b) Cách 1: Sử dụng công thức \({S_{xq}} = \frac{1}{2}C.d\).
Diện tích xung quanh của hình chóp tứ giác đều là:
\({S_{xq}} = \frac{1}{2}.C.d = \frac{1}{2}.\left( {5.4} \right).9,68 = 96,8\;\;\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Diện tích tất cả các mặt của hình chóp tứ giác đều là:
\(96,8 + {5^2} = 121,8\;\;\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
Cách 2: Sử dụng công thức \({S_{xq}} = 4.\)S mặt bên .
Diện tích xung quanh của hình chóp tứ giác đều là:
\({S_{xq}} = 4.\)S mặt bên \( = 4.\frac{1}{2}.5.9,68 = 96,8\;\;\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Diện tích tất cả các mặt của hình chóp tứ giác đều là:
\(96,8 + {5^2} = 121,8\;\;\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)