Xe khối lượng 1 tấn chuyển động thẳng đều lên dốc dài 200 — Không quảng cáo

Phương pháp giải

+ Công thức tính lực ma sát: \({F_{ms}} = \mu .N\)

+ Định luật 2 Newton: \(\sum {\overrightarrow F  = m.\overrightarrow a } \)

+ Định luật 1 Newton: Nếu không chịu tác dụng của lực nào hoặc chịu tác dụng của các lực có hợp lực bằng không, thì vật đang đứng yên sẽ tiếp tục đứng yên, đang chuyển động sẽ tiếp tục chuyển động thẳng đều.

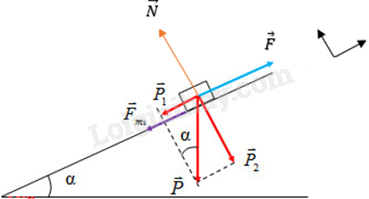
Chọn hệ trục tọa độ như hình vẽ:

Áp dụng định luật 2 Newton:

\(\overrightarrow {{F_{ms}}}  + \overrightarrow P  + \overrightarrow N  + \overrightarrow F  = m.\overrightarrow a \)

\( \Leftrightarrow \overrightarrow {{F_{ms}}}  + \overrightarrow P  + \overrightarrow N  + \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  = m.\overrightarrow a \)                    (*)

Chiếu (*) lên Ox, Oy, ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}N = {P_2} = P.\cos \alpha \\F - {F_{ms}} - {P_1} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}N = {P_2} = P.\cos \alpha \\F - \mu N - mg\sin \alpha  = 0\end{array} \right.\\ \Rightarrow F = \mu N + mg\sin \alpha  = \mu mg\cos \alpha  + mg\sin \alpha \\ = mg.(\mu \cos \alpha  + \sin \alpha )\\ = {10^3}.10.(0,01.\frac{{\sqrt {{{200}^2} - {{10}^2}} }}{{200}} + \frac{1}{{20}}) = 600(N)\end{array}\)