Bài 1.36 trang 41 SGK Toán 11 tập 1 - Kết nối tri thức
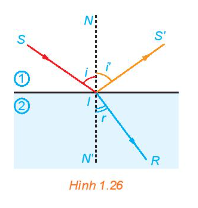
Khi một tia sáng truyền từ không khi vào mặt nước thì một phần tia sáng bị phản xạ trên bề mặt, phần còn lại bị khúc xạ như trong Hình 1.26.
Đề bài
Khi một tia sáng truyền từ không khi vào mặt nước thì một phần tia sáng bị phản xạ trên bề mặt, phần còn lại bị khúc xạ như trong Hình 1.26. Góc tới i liên hệ với góc khúc xạ r bởi Định luật khúc xạ ánh sáng
\(\frac{{\sin i}}{{\sin r}} = \frac{{{n_2}}}{{{n_1}}}\)
Ở đây, \({n_1}\) và \({n_2}\) tương ứng là chiết suất của môi trường 1 (không khí) và môi trường 2 (nước). Cho biết góc tới \(i = {50^0}\), hãy tính góc khúc xạ, biết rằng chiết suất của không khí bằng 1 còn chiết suất của nước là 1,33.
Phương pháp giải - Xem chi tiết
Dùng công thức \(\frac{{\sin i}}{{\sin r}} = \frac{{{n_2}}}{{{n_1}}}\) để tìm sin r. Từ đó, tìm số đo góc khúc xạ.
Lời giải chi tiết
Theo bài ra ta có: \(i = 50^\circ ,{\rm{ }}{n_1}\; = 1,{\rm{ }}{n_2}\; = 1,33\) thay vào \(\frac{{\sin i}}{{\sin r}} = \frac{{{n_2}}}{{{n_1}}}\) ta được:
\(\begin{array}{l}\frac{{\sin {{50}^o}}}{{\sin r}} = \frac{{1,33}}{1}\,(r \ne 0)\\ \Rightarrow \sin r = \frac{{\sin {{50}^o}}}{{1,33}} \approx 0,57597\,\,(TM)\\ \Leftrightarrow \left[ \begin{array}{l}r \approx {35^o}10' + k{360^o}\\r \approx {180^o} - {35^o}10' + k{360^o}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}r \approx {35^o}10' + k{360^o}\\r \approx {144^o}50' + k{360^o}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Mà \({0^o} < r < {90^o} \Rightarrow r \approx {35^o}10'\)
Vạy góc khúc xạ \(r \approx {35^o}10'\)