Bài 1 trang 15 SGK Toán 11 tập 1 - Cánh diều — Không quảng cáo

Đề bài

Xác định vị trí các điểm M, N, P trên đường tròn lượng giác sao cho số đo của các góc lượng giác $\left( {OA,OM} \right),\,\left( {OA,ON} \right),\,\left( {OA,OP} \right)$ lần lượt bằng $\frac{\pi }{2};\,\,\frac{{7\pi }}{6};\,\, - \frac{\pi }{6}$. Chứng minh rằng tam giác MNP là tam giác đều.

Lời giải chi tiết

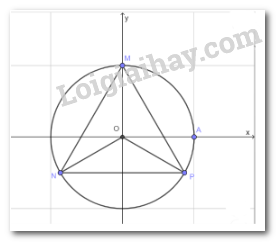
$\begin{array}{l}(OM,ON) = (OA,ON) - (OA,OM) = \frac{{2\pi }}{3}\\ \Rightarrow \widehat {MON} = {120^0}\\\widehat {MOP} = \widehat {MOA} + \widehat {AOP} = {90^0} + {30^0} = {120^0}\\ \Rightarrow \widehat {NOP} = {360^0} - {120^0} - {120^0} = {120^0}\end{array}$

Cung MP = cung NP = cung NM

$\Rightarrow MP = NP = NM$

$\Rightarrow \Delta MNP$ đều