Bài 4. Biểu thức chứa chữ (tiết 2) trang 12 Vở thực hành Toán 4
Chu vi P của hình chữ nhật có chiều dài a, chiều rộng b (cùng đơn vị đo) được tính theo công thức .... Tính giá trị của biểu thức a + b x 2 với a = 8, b = 2.
Câu 1
Hoàn thành bảng sau (theo mẫu):
Chu vi P của hình chữ nhật có chiều dài a, chiều rộng b (cùng đơn vị đo) được tính theo công thức P = (a + b) x 2
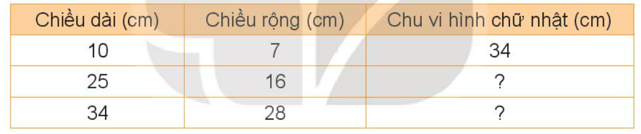
Hãy tính chu vi hình chữ nhật theo kích thước như bảng sau:
Phương pháp giải:
Thay các số đo chiều dài, chiều rộng vào biểu thức P = (a + b) x 2 rồi tính giá trị biểu thức đó.
Lời giải chi tiết:
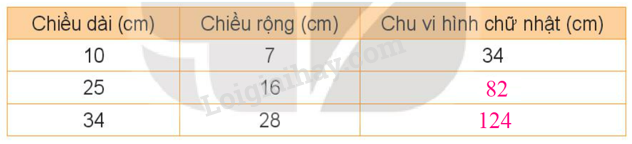
Nếu a = 10, b = 7 thì chu vi P = (a + b) x 2 = (10 + 7) x 2 = 34 (cm)
Nếu a = 25, b = 16 thì chu vi P = (a + b) x 2 = (25 + 16) x 2 = 82 (cm)
Nếu a = 34 , b = 28 thì chu vi P = (a + b) x 2 = (34 + 28) x 2 = 124 (cm)
Ta điền như sau:
Câu 2
a) Tính giá trị của biểu thức a + b x 2 với a = 8, b = 2.
b) Tính giá trị của biểu thức (a + b) : 2 với a = 15, b = 27.
Phương pháp giải:
- Thay chữ bằng số vào biểu thức đã cho rồi tính giá trị của biểu thức đó.
- Áp dụng các quy tắc tính giá trị biểu thức:
+ Biểu thức có dấu ngoặc thì tính trong ngoặc trước, ngoài ngoặc sau.
+ Biểu thức có các phép tính cộng, trừ, nhân, chia thì thực hiện phép nhân, chia trước; thực hiện phép cộng, trừ sau.
Lời giải chi tiết:
a) Với a = 8, b = 2 thì a + b x 2 = 8 + 2 x 2
= 8 + 4
= 12
b) Với a = 15, b = 27 thì (a + b) : 2 = (15 + 27) : 2
= 42 : 2
= 21
Câu 3
Viết số thích hợp vào chỗ chấm.
Quãng đường ABCD gồm ba đoạn như hình vẽ dưới đây.

a) Độ dài quãng đường ABCD với m = 4 km, n = 7 km là ......... km.
b) Độ dài quãng đường ABCD với m = 5 km, n = 9 km là ......... km.
Phương pháp giải:
- Độ dài quãng đường ABCD = m + 6 + n
- Thay chữ bằng số vào biểu thức đã cho rồi tính giá trị của biểu thức đó.
Lời giải chi tiết:
a) Độ dài quãng đường ABCD với m = 4 km, n = 7 km là 17 km.
b) Độ dài quãng đường ABCD với m = 5 km, n = 9 km là 20 km.
Câu 4
a) Hoàn thành bảng sau:

b) Viết số thích hợp vào chỗ chấm.
Trong ba giá trị của biểu thức tìm được ở câu a, với m bằng ......... thì biểu thức 12 : (3 – m) có giá trị lớn nhất.
Phương pháp giải:
a) Thay chữ bằng số vào biểu thức đã cho rồi tính giá trị của biểu thức đó.
b) Dựa vào câu a, xác định m để biểu thức thức 12 : (3 – m) có giá trị lớn nhất.
Lời giải chi tiết:
a) Với m = 0 thì 12 : (3 – m) = 12 : (3 – 0) = 12 : 3 = 4
Với m = 1 thì 12 : (3 – m) = 12 : (3 – 1) = 12 : 2 = 6
Với m = 2 thì 12 : (3 – m) = 12 : (3 – 2) = 12 : 1 = 12

b) Trong ba giá trị của biểu thức tìm được ở câu a, với m bằng 2 thì biểu thức 12 : (3 – m) có giá trị lớn nhất.