Bài 5.15 trang 147 SGK Toán 11 tập 1 - Cùng khám phá
Một du học sinh ở nước ngoài đã tìm hiểu mức lương của nhận viên thuộc một công ty và thu được Bảng 5.35 dưới đây. Nếu xét về lương thì có hay không sự bất bình đẳng giữa nam giới và nữ giới làm việc ở công ty này? Giải thích câu trả lời bằng cách dựa vào các tham số đo xu thế trung tâm (trung bình, trung vị, mốt) của mẫu số liệu.
Đề bài
Một du học sinh ở nước ngoài đã tìm hiểu mức lương của nhận viên thuộc một công ty và thu được Bảng 5.35 dưới đây. Nếu xét về lương thì có hay không sự bất bình đẳng giữa nam giới và nữ giới làm việc ở công ty này? Giải thích câu trả lời bằng cách dựa vào các tham số đo xu thế trung tâm (trung bình, trung vị, mốt) của mẫu số liệu.

Phương pháp giải - Xem chi tiết
+) \(\overline x \) của mẫu số liệu ghép nhóm được tính theo công thức
\(\overline x = \frac{1}{N}\left( {{c_1}{n_1} + {c_2}{n_2} + ... + {c_k}{n_k}} \right)\) với \({c_k},{n_k}\) lần lượt là giá trị đại diện và tần số của nhóm thứ k
\({c_k}\) là trung bình cộng của đầu mút trái và đầu mút phải của nhóm đó.
+) Trung vị \({M_e} = {L_m} + \frac{{\frac{N}{2} - T}}{{{n_m}}}.h\) trong đó \({L_m},{n_m},h\) lần lượt là đầu mút trái, tần số và độ dài của nhóm chứa trung vị. \(T\) là tần số tích lũy của nhóm ngay trước nhóm chứa trung vị.
Nhóm chứa trung vị của mẫu số liệu là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{N}{2}\) , trong đó \(N\) là cỡ mẫu.
+) Công thức tìm mốt của mẫu số liệu ghép nhóm là \({M_0} = {L_m} + \frac{a}{{a + b}}.h\)
Lời giải chi tiết
+) Tính trung bình
Để ngắn gọn, ta lập bảng sau
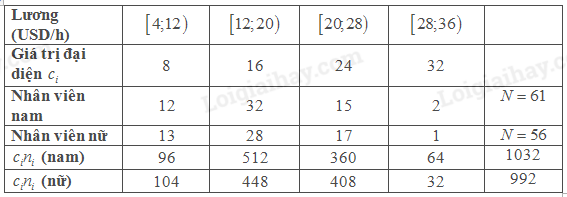
Ta có lương trung bình của nam là \(\overline x = \frac{{1032}}{{61}} \approx 16,9\) USD
Lương trung bình của nữ là \(\overline x = \frac{{992}}{{59}} \approx 16,8\) USD
+) Tìm trung vị
Để ngắn gọn, ta lập bảng sau
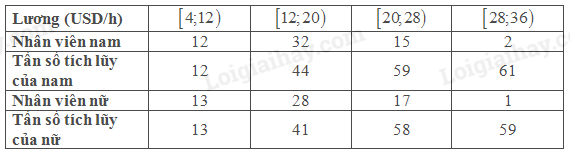
Đối với nam thì \(\frac{N}{2} = \frac{{61}}{2} = 30,5\). Nhóm đầu tiên có tần số tích lũy lớn hơn bằng \(30,5\) là nhóm \(\left[ {12;20} \right)\) và đây là nhóm chứa trung bị với \({L_m} = 12,\) tần số \({n_m} = 32\), \(h = 20 - 12 = 8\), tần số tích lũy của nhóm trước nhóm chứa trung vị là \(T = 12\)
Áp dụng công thức tính trung vị ta có \({M_e} = {L_m} + \frac{{\frac{N}{2} - T}}{{{n_m}}}.h = 12 + \frac{{30,5 - 12}}{{32}}.8 \approx 16,6\)
Đối với nữa thì \(\frac{N}{2} = \frac{{59}}{2} = 29,5\). Nhóm đầu tiên có tần số tích lũy lớn hơn bằng \(29,5\) là nhóm \(\left[ {12;20} \right)\) và đây là nhóm chứa trung bị với \({L_m} = 12,\) tần số \({n_m} = 28\), \(h = 20 - 12 = 8\), tần số tích lũy của nhóm trước nhóm chứa trung vị là \(T = 13\)
Áp dụng công thức tính trung vị ta có \({M_e} = {L_m} + \frac{{\frac{N}{2} - T}}{{{n_m}}}.h = 12 + \frac{{29,5 - 13}}{{28}}.8 \approx 16,7\)
+) Tìm mốt
Đối với nam thì nhóm chứa mốt là \(\left[ {12;20} \right)\) với \({L_m} = 12;h = 20 - 12 = 8\)
\(a = 32 - 12 = 20,b = 32 - 15 = 17\)
Áp dụng công thức tính mốt ta có \({M_0} = {L_m} + \frac{a}{{a + b}}.h = 12 + \frac{{20}}{{20 + 17}}.8 \approx 16,3\)
Đối với nam thì nhóm chứa mốt là \(\left[ {12;20} \right)\) với \({L_m} = 12;h = 20 - 12 = 8\)
\(a = 28 - 13 = 15,b = 28 - 17 = 11\)
Áp dụng công thức tính mốt ta có \({M_0} = {L_m} + \frac{a}{{a + b}}.h = 12 + \frac{{15}}{{15 + 11}}.8 \approx 16,6\)
Dựa vào các tham số đo xu thế trung tâm ta nhận thấy xét về lương thì không có sự bất bình đẳng giữa nam giới và nữ giới.