Bài 7.30 trang 63 SGK Toán 11 tập 2 - Kết nối tri thức
Cho khối chóp đều S.ABCD, đáy có cạnh 6 cm. Tính thể tích của khối chóp đó trong các trường hợp sau.
Đề bài
Cho khối chóp đều S.ABCD, đáy có cạnh 6 cm. Tính thể tích của khối chóp đó trong các trường hợp sau.
a) Cạnh bên tạo với mặt đáy một góc bằng \({60^0}.\)
b) Mặt bên tạo với mặt đáy một góc bằng \({45^0}.\)
Phương pháp giải - Xem chi tiết
- Thế tích khối chóp \(V = \frac{1}{3}h.S\)
- Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của đường thẳng trên mặt phẳng đó.
- Góc giữa hai mặt phẳng là góc giữa 2 đường thẳng trong hai mặt phẳng vuông góc với giao tuyến tại cùng một điểm.
Lời giải chi tiết
a)
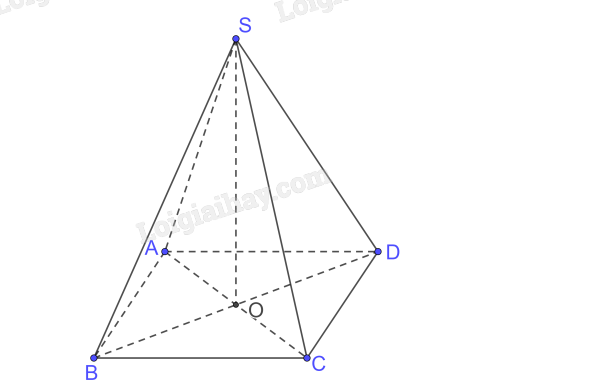
Gọi \(AC \cap BD = \left\{ O \right\}\) mà S.ABCD đều nên \(SO \bot \left( {ABCD} \right)\)
\( \Rightarrow \) O là hình chiếu của S trên (ABCD)
C là hình chiếu của C trên (ABCD)
\( \Rightarrow \) OC là hình chiếu của SC trên (ABCD)
\( \Rightarrow \) (SC, (ABCD)) = (SC, OC) \( = \widehat {SCO}\)
Mà cạnh bên tạo với mặt đáy một góc bằng \({60^0}.\)
\( \Rightarrow \widehat {SCO} = {60^0}\)
Xét tam giác ABC vuông tại B có \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{6^2} + {6^2}} = 6\sqrt 2 \left( {cm} \right)\)
\( \Rightarrow OC = \frac{{AC}}{2} = \frac{{6\sqrt 2 }}{2} = 3\sqrt 2 \left( {cm} \right)\)
Xét tam giác SOC vuông tại O có
\(\tan \widehat {SCO} = \frac{{SO}}{{OC}} \Rightarrow SO = 3\sqrt 2 .\tan {60^0} = 3\sqrt 6 \left( {cm} \right)\)
\({S_{ABCD}} = {6^2} = 36\left( {c{m^2}} \right)\)
Vậy khối chóp có thể tích \(V = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}.3\sqrt 6 .36 = 36\sqrt 6 \left( {c{m^3}} \right)\)
b)
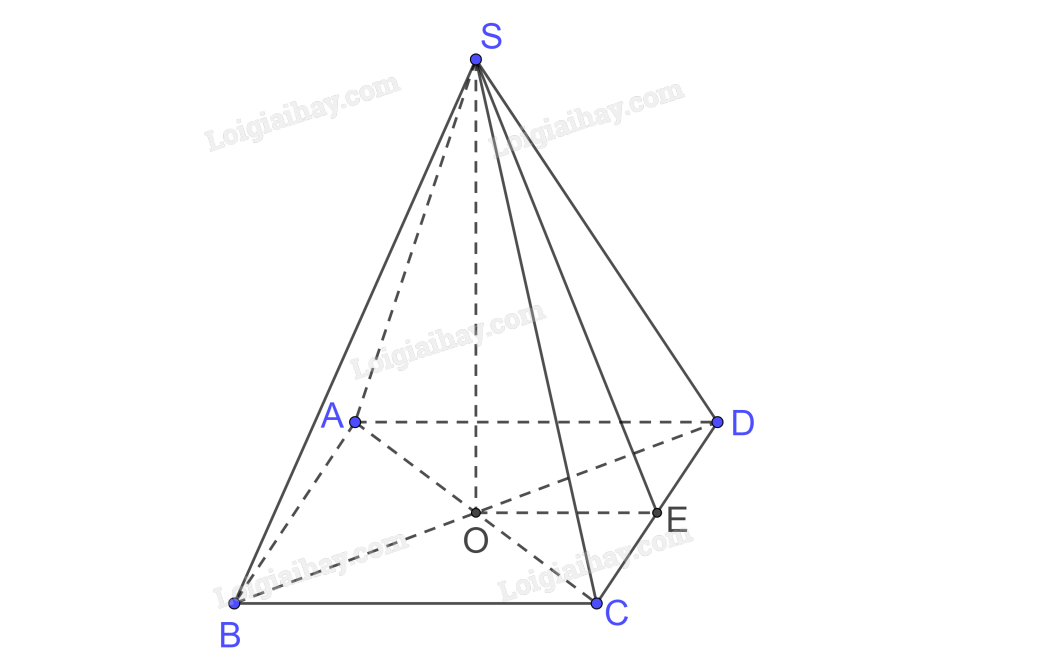
Trong (ABCD) kẻ \(OE \bot CD\)
\(\begin{array}{l}SO \bot CD\left( {SO \bot \left( {ABCD} \right)} \right)\\ \Rightarrow CD \bot \left( {SOE} \right),SE \subset \left( {SOE} \right) \Rightarrow CD \bot SE,OE \bot CD,\left( {SCD} \right) \cap \left( {ABCD} \right) = CD\\ \Rightarrow \left( {\left( {SCD} \right),\left( {ABCD} \right)} \right) = \left( {SE,OE} \right) = \widehat {SEO}\end{array}\)
Mà mặt bên tạo với mặt đáy một góc bằng \({45^0}.\)
\( \Rightarrow \widehat {SEO} = {45^0}\)
Ta có \(\left. \begin{array}{l}OE \bot CD\\AD \bot CD\end{array} \right\} \Rightarrow OE//AD\) mà O là trung điểm AC nên OE là đường trung bình tam giác ACD.
\( \Rightarrow OE = \frac{{AD}}{2} = \frac{6}{2} = 3\left( {cm} \right)\)
Xét tam giác SOE vuông tại O có
\(\tan \widehat {SEO} = \frac{{SO}}{{OE}} \Rightarrow SO = 3.\tan {45^0} = 3\left( {cm} \right)\)
Vậy khối chóp có thể tích \(V = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}.3.36 = 36\left( {c{m^3}} \right)\)