Bài tập 10 trang 128 Tài liệu dạy – học Toán 7 tập 2 — Không quảng cáo

Đề bài

Cho tam giác ABC có ba đường cao AD, BE, CF . Biết AD = BE = CF. Chứng minh rằng tam giác ABC đều.

Lời giải chi tiết

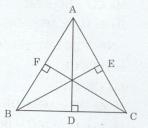
Xét ∆ACF ($\widehat F = 90^\circ$) và ∆ADC ($\widehat D = 90^\circ$) có AC (cạnh chung) và CF = AD (gt)

Do đó: ∆ACF = ∆CAD (cạnh huyền – cạnh góc vuông).

$\Rightarrow \widehat {CAF} = \widehat {ACD}$ hay $\widehat {CAB} = \widehat {ACB}$ (1)

Xét ∆BEC ($\widehat E = 90^\circ$) và ∆BFC ($\widehat F = 90^\circ$)

Ta có: BC (cạnh chung)

BE = CF (gt)

Do đó: ∆BEC = ∆CFB (cạnh huyền – cạnh góc vuông).

$\Rightarrow \widehat {ACB} = \widehat {ABC}$ (2)

Xét ∆BEA ($\widehat E = 90^\circ$) và ∆ABD ($\widehat D = 90^\circ$) có AB (cạnh chung) và BE = AD (gt)

Do đó: ∆BEA = ∆ADB (cạnh huyền – cạnh góc vuông) $\Rightarrow \widehat {BAC} = \widehat {ABC}$ (3)

Từ (1), (2) và (3) $\Rightarrow \widehat {CAB} = \widehat {ACB} = \widehat {ABC}$ => ∆ABC đều.