Bài tập 3 trang 156 Tài liệu dạy – học Toán 7 tập 1
Giải bài tập Ở hình 55 cho biết
Đề bài
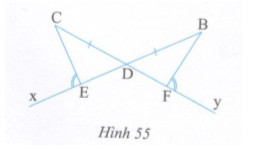
Ở hình 55 cho biết \(DC = DB,\,\,\widehat {CEx} = \widehat {BFy}.\) Chứng minh rằng \(\Delta DEC = \Delta DFB\)
Lời giải chi tiết
Ta có: \(\widehat {CEx} = \widehat {ECD} + \widehat {CDE}\) và \(\widehat {BFy} = \widehat {FBD} + \widehat {BDF}\) (góc ngoài tam giác).
Mà \(\widehat {CEx} = \widehat {BFy}(gt);\widehat {CDE} = \widehat {BDF}\) (đối đỉnh) nên \(\widehat {ECD} = \widehat {FBD}\)
Xét tam giác DEC và DFB có:
\(\widehat {EDC} = \widehat {FDB}\) (hai góc đối đỉnh)
CD = BD (gt)
\(\widehat {ECD} = \widehat {FBD}(cmt)\)
Do đó: \(\Delta DEC = \Delta DFB(g.c.g)\)
Cùng chủ đề:
Bài tập 3 trang 156 Tài liệu dạy – học Toán 7 tập 1