Bài tập 8 trang 116 Tài liệu dạy – học Toán 7 tập 1 — Không quảng cáo

Đề bài

Cho hai đường thẳng xx’ và yy’ cắt nhau tại O. Gọi Ot là tia phân giác của góc xOy; vẽ tia Ot’ là tia phân giác của góc x’Oy’. Hãy chứng tỏ rằng Ot’ là tia đối của tia Ot.

Lời giải chi tiết

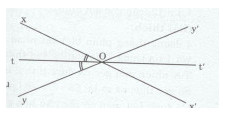
Ta có: \(\widehat {xOy} = \widehat {x'Oy'}\)  (hai góc đối đỉnh).

\(\widehat {xOt} = {1 \over 2}\widehat {xOy}\)  (Ot là tia phân giác của góc xOy)

\(\widehat {x'Ot'} = {1 \over 2}\widehat {x'Oy'}\)  (Ot’ là tia phân giác của góc x’Oy’).

Do đó: \(\widehat {xOt} = \widehat {x'Ot'}\)

Mà \(\widehat {xOt'} + \widehat {x'Ot'} = {180^0}\)  (hai góc kề bù)

Nên \(\widehat {xOt'} + \widehat {xOt} = {180^0}\)

Suy ra hai tia Ot và Ot’ là hai tia đối nhau.