Cách tính xác suất của biến cố bằng tỉ số
Tính xác suất bằng tỉ số như thế nào? Các bước tính xác suất bằng tỉ số là gì?
1. Lý thuyết
- Công thức tính xác suất bằng tỉ số
Giả thiết rằng các kết quả có thể của một hành động hay thực nghiệm là đồng khả năng. Khi đó, xác suất của biến cố E, kí hiệu là P(E), bằng tỉ số giữa số kết quả thuận lợi cho biến cố E và tổng số kết quả có thể.
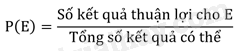
- Các bước tính xác suất bằng tỉ số
Việc tính xác suất của một biến cố E trong một hành động hay thực nghiệm đồng khả năng sẽ gồm các bước sau:
Bước 1. Đếm các kết quả có thể (thường bằng cách liệt kê);
Bước 2. Chỉ ra các kết quả có thể là đồng khả năng;
Bước 3. Đếm các kết quả thuận lợi cho biên cố E;
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E và tổng số kết quả có thể.
- Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản:
+ Xác suất của biến cố trong trò chơi tung đồng xu

Trong trò chơi tung đồng xu, ta có:
- Xác suất của biến cố “Mặt xuất hiện của đồng xu là mặt N” bằng \(\frac{1}{2}\).
- Xác suất của biến cố “Mặt xuất hiện của đồng xu là mặt S” bằng \(\frac{1}{2}\).
+ Xác suất của biến cố trong trò chơi vòng quay số
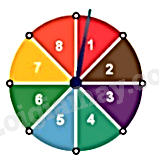
Trong trò chơi vòng quay số đã nêu, nếu k là số kết quả thuận lợi cho một biến cố thì xác suất của biến cố đó bằng \(\frac{k}{8}\).
+ Xác suất của biến cố trong trò chơi chọn ngẫu nhiên một đối tượng từ một nhóm đối tượng
Trong trò chơi ngẫu nhiên, một đối tượng từ một nhóm đối tượng, xác suất của một biến cố bằng tỉ số của số kết quả thuận lợi cho biến cố và số các kết quả có thể xảy ra đối với đối tượng được chọn ra.

2. Ví dụ minh họa
Ví dụ 1. Gieo một con xúc xắc.
Các kết quả có thể của hành động trên là 1, 2, 3, 4, 5, 6 chấm. Có 6 kết quả có thể.
Biến cố E: “Gieo được số chấm lẻ” xảy ra khi gieo được các số lẻ. Do đó các kết quả thuận lợi cho biến cố E là 1, 3, 5. Có 3 kết quả thuận lợi
Xác suất của biến cố E là: \(P(E) = \frac{3}{6} = \frac{1}{2}\).
Ví dụ 2. Hình bên mô tả một đĩa tròn bằng bìa cứng được chia làm tám phần bằng nhau và ghi các số 1; 2; 3; 4; 5; 6; 7; 8. Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa . Quay đĩa tròn một lần.

Tính xác suất của các biến cố sau :
a/ “ Mũi tên chỉ vào hình quạt ghi số nhỏ hơn 3”.
b/ “ Mũi tên chỉ vào hình quạt ghi số nhỏ hơn 5”.
c/ “ Mũi tên chỉ vào hình quạt ghi số là ước của 6”.
Lời giải:
a/ Có 2 kết quả thuận lợi cho biến cố “ Mũi tên chỉ vào hình quạt ghi số nhỏ hơn 3” đó là 1;2
Vì thế xác suất của biến cố đó là \(\frac{2}{8} = \frac{1}{4}\) .
b/ Có 4 kết quả thuận lợi cho biến cố “ Mũi tên chỉ vào hình quạt ghi số nhỏ hơn 5” đó là 1;2; 3; 4.
Vì thế xác suất của biến cố đó là \(\frac{4}{8} = \frac{1}{2}\) .
c/ Có 4 kết quả thuận lợi cho biến cố “ Mũi tên chỉ vào hình quạt ghi số là ước của 6” đó là 1;2; 3; 6.
Vì thế xác suất của biến cố đó là \(\frac{4}{8} = \frac{1}{2}\) .