Đề kiểm tra 15 phút - Đề số 1 - Bài 1 - Chương 1 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 1 - Bài 1 - Chương 1 - Hình học 9
Đề bài
Cho ∆ABC vuông tại A có \(AB = 30cm\), đường cao \(AH = 24cm\).
a. Tính BH, BC, AC.
b. Đường thẳng vuông góc với AB tại B cắt tia AH tại D. Tính BD.
Phương pháp giải - Xem chi tiết
Sử dụng định lý Pytago và hệ thức lượng trong tam giác vuông.
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Khi đó ta có các hệ thức sau:
+) \(A{B^2} = BH.BC\) và \(A{C^2} = CH.BC\)
+) \(H{A^2} = HB.HC\)
+) \(AB.AC = BC.AH\)
+) \(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}\)
+) \(B{C^2} = A{B^2} + A{C^2}\) (Định lí Pitago).
Lời giải chi tiết
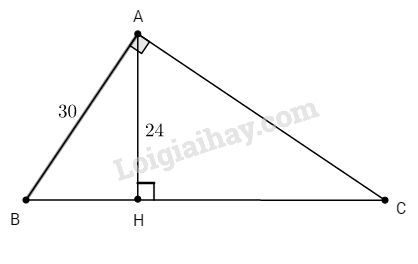
a. Ta có: ∆AHB vuông tại H. Theo định lí Pi-ta-go :
\(\eqalign{ & B{H^2} = A{B^2} - A{H^2} \cr & \Rightarrow BH = \sqrt {A{B^2} - A{H^2}} \cr&\;\;\;\;\;\;\;\;\;\;\;\;= \sqrt {{{30}^2} - {{24}^2}} = 18\,\left( {cm} \right) \cr} \)
Lại có ∆ABC vuông tại A
\(A{B^2} = BC.BH\) (định lí 1)
\( \Rightarrow BC = {{A{B^2}} \over {BH}}\)\(\; = {{{{30}^2}} \over {18}} = 50\,cm\)
Do đó \(A{C^2} = B{C^2} - A{B^2}\) (định lí Pi-ta-go)
\( \Rightarrow AC = \sqrt {B{C^2} - A{B^2}} \)\(\;= \sqrt {{{50}^2} - {{30}^2}} = 40\,\left( {cm} \right)\)
b.
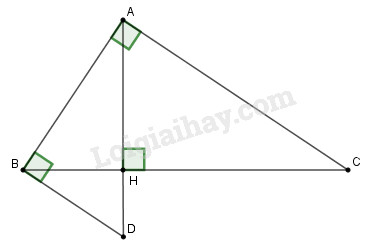
Ta có: ∆ABD vuông tại B, đường cao là BH nên:
\(A{B^2} = AD.AH\) (định lí 1)
\( \Rightarrow AD = {{A{B^2}} \over {AH}} = {{{{30}^2}} \over {24}} = 37,5\,\left( {cm} \right)\)
Do đó \(HD = AD - AH = 37,5 - 24 \)\(\;= 13,5\,\left( {cm} \right)\)
\( \Rightarrow B{D^2} = AD.HD\) (định lí 1)
\( \Rightarrow BD = \sqrt {AD.HD} = \sqrt {37,5.13,5} \)\(\;= 22,5\,\left( {cm} \right)\)