Đề kiểm tra 15 phút - Đề số 1 - Bài 1 - Chương 4 - Đại số 9 — Không quảng cáo

Đề bài

Bài 1 : Cho hàm số $y = a{x^2}.$

a) Xác định a, biết rằng đồ thị (P ) của hàm số đi qua điểm $A(2; − 4).$

b) Vẽ đồ thị của hàm số với a vừa tìm được ở câu trên.

Bài 2 : Cho hàm số : $y = f\left( x \right) =  - {3 \over 2}{x^2}.$ So sánh $f\left( {{{2 + \sqrt 5 } \over 4}} \right)$ và $f\left( {{{2 + \sqrt 6 } \over 4}} \right).$

Bài 3 : Tìm giá trị nhỏ nhất của hàm số : $y = \left( {{m^2} + 1} \right){x^2}.$

LG bài 1

Phương pháp giải:

a.Thế tọa độ của điểm A vào hàm số ta tìm được a

b.

Bước 1: Tìm tập xác định của hàm số.

Bước 2: Lập bảng giá trị

Bước 3: Vẽ đồ thị và kết luận.

Lời giải chi tiết:

Bài 1: a) $A \in (P)  \Rightarrow  - 4 = a.{\left( 2 \right)^2} \Rightarrow a =  - 1$

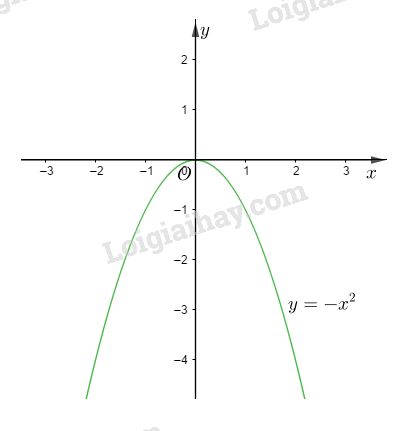
Ta có : $y =  - {x^2}.$

b) Vẽ đồ thị $y =  - {x^2}.$

TXĐ: $x \in \mathbb{R}$

Bảng giá trị :

Đồ thị (P) của hàm số là một parabol có đỉnh là O và trục Oy là trục đối xứng ( Xem hình vẽ).

LG bài 2

Phương pháp giải:

Chỉ ra hàm số nghịch biến(do a<0) khi x> 0 rồi đi so sánh

Lời giải chi tiết:

Bài 2: Nếu $a =  - {3 \over 2} < 0$ thì hàm số nghịch biến khi $x > 0$.

Vậy $a =  - {3 \over 2}$ thì $0 < {{2 + \sqrt 5 } \over 4} < {{2 + \sqrt 6 } \over 4}$$\; \Rightarrow f\left( {{{2 + \sqrt 5 } \over 4}} \right) > f\left( {{{2 + \sqrt 6 } \over 4}} \right).$

LG bài 3

Phương pháp giải:

Từ ${m^2} + 1 > 0$, với mọi m thuộc R ta suy ra GTNN của hàm số

Lời giải chi tiết:

Bài 3: Ta có : ${m^2} + 1 > 0$, với mọi m thuộc R . Vậy giá trị nhỏ nhất của hàm số là 0, khi $x = 0.$