Đề kiểm tra giữa kì 1 Toán 9 - Đề số 5 có lời giải chi tiết
Đề kiểm tra giữa kì 1 Toán 9 - Đề số 5 có lời giải chi tiết
Đề bài
Bài 1 (1,5 điểm):
1) Tính giá trị biểu thức \(P = \sqrt {125} + \sqrt {20} - \sqrt {180} \).
2) Tìm giá trị \(x\) thực biết: \(\sqrt {x - 1} + \sqrt {9x - 9} - \sqrt {4x - 4} = 4\).
Bài 2 (2 điểm): Rút gọn các biểu thức
1) \(A = \frac{1}{{2 - \sqrt 3 }} + \frac{1}{{2 + \sqrt 3 }}\) 2) \(B = \sqrt {5 + 2\sqrt {{{\left( {1 - \sqrt 2 } \right)}^2}} } \) 3) \(C = \frac{{x + \sqrt x - 2}}{{\sqrt x + 2}}\) (với \(x \ge 0\))
Bài 3 (3 điểm):
Cho các biểu thức: \(A = \frac{{x - 4}}{{\sqrt x - 2}}\) và \(B = \frac{2}{{\sqrt x - 2}} + \frac{3}{{\sqrt x + 2}} - \frac{{x - 5\sqrt x + 2}}{{4 - x}}\) với \(x \ge 0;x \ne 4\)
1) Tính giá trị của \(A\) khi \(x = 49\).
2) Rút gọn \(B\).
3) Với \(x > 4\), tìm giá trị nhỏ nhất của biểu thức \(P = A.B\).
Bài 4 (3 điểm):
Cho \(\Delta ABC\) vuông tại \(A,\) đường cao \(AH,\,\,AB = 3\,cm,\,\,BC = 6\,cm.\) Gọi \(E,\,\,F\) lần lượt là hình chiếu vuông góc của \(H\) trên \(AB\) và \(AC.\)
a) Giải \(\Delta ABC.\)
b) Tính \(AH\) và chứng minh \(EF = AH.\)
c) Tính \(EA.EB + AF.FC.\)
Bài 5 (0,5 điểm): Tìm giá trị nhỏ nhất của biểu thức \(A = \frac{1}{{{x^2} + {y^2}}} + \frac{2}{{xy}} + 4xy\) với \(x > 0;y > 0;x + y \le 1\).
Lời giải chi tiết
Bài 1
Phương pháp:
1) Rút gọn căn bậc hai bằng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\;\,khi\,\,A \ge 0\\ - A\sqrt B \,\;\,khi\,\,A < 0\end{array} \right..\)
2) Tìm điều kiện xác định sau đó giải phương trình bằng phương pháp đưa phương trình về dạng phương trình tích sau đó bình phương hai vế.
Cách giải:
1) Tính giá trị biểu thức \(P = \sqrt {125} + \sqrt {20} - \sqrt {180} \) .
\(\begin{array}{l}P = \sqrt {125} + \sqrt {20} - \sqrt {180} = \sqrt {{5^3}} + \sqrt {4.5} - \sqrt {36.5} \\\,\,\,\,\,\, = \sqrt {{5^2}.5} + \sqrt {{2^2}.5} - \sqrt {{6^2}.5} = 5\sqrt 5 + 2\sqrt 5 - 6\sqrt 5 \\\,\,\,\,\,\, = \sqrt 5 .\end{array}\)
Vậy \(P = \sqrt 5 \).
2) Tìm giá trị \(x\) thực biết: \(\sqrt {x - 1} + \sqrt {9x - 9} - \sqrt {4x - 4} = 4\) .
Điều kiện xác định : \(\left\{ \begin{array}{l}x - 1 \ge 0\\9x - 9 \ge 0\\4x - 4 \ge 0\end{array} \right. \Rightarrow x - 1 \ge 0 \Rightarrow x \ge 1\)
\(\begin{array}{l}\,\,\,\,\,\,\,\sqrt {x - 1} + \sqrt {9x - 9} - \sqrt {4x - 4} = 4\\ \Leftrightarrow \sqrt {x - 1} + \sqrt {9\left( {x - 1} \right)} - \sqrt {4\left( {x - 1} \right)} = 4\\ \Leftrightarrow \sqrt {x - 1} + 3\sqrt {x - 1} - 2\sqrt {x - 1} = 4\\ \Leftrightarrow 2\sqrt {x - 1} = 4\\ \Leftrightarrow \sqrt {x - 1} = 2\\ \Leftrightarrow x - 1 = {2^2} = 4\\ \Leftrightarrow x = 5\,\,\,\,\,\left( {tmdk} \right)\end{array}\)
Vậy phương trình có nghiệm \(x = 5\).
Bài 2
Phương pháp:
1) Quy đồng mẫu của các biểu thức để rút gọn
2) Rút gọn căn bậc hai bằng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\;\,khi\,\,A \ge 0\\ - A\sqrt B \,\;\,khi\,\,A < 0\end{array} \right..\)
3) Phân tích đa thức trên tử số thành nhân tử và rút gọn với mẫu số.
Cách giải:
\(1)\,\,\,A = \frac{1}{{2 - \sqrt 3 }} + \frac{1}{{2 + \sqrt 3 }} = \frac{{2 + \sqrt 3 + 2 - \sqrt 3 }}{{\left( {2 - \sqrt 3 } \right)\left( {2 + \sqrt 3 } \right)}} = \frac{4}{{{2^2} - 3}} = 4\)
Vậy \(A = 4.\)
\(\begin{array}{l}2)\,\,B = \sqrt {5 + 2\sqrt {{{\left( {1 - \sqrt 2 } \right)}^2}} } = \sqrt {5 + 2.\left( {\sqrt 2 - 1} \right)} \\\,\,\,\,\,\,\,\,\,\,\, = \sqrt {5 + 2\sqrt 2 - 2} = \sqrt {3 + 2\sqrt 2 } \\\,\,\,\,\,\,\,\,\,\,\, = \sqrt {{{\left( {\sqrt 2 + 1} \right)}^2}} = \sqrt 2 + 1.\end{array}\)
Vậy \(B = \sqrt 2 + 1.\)
\(\begin{array}{l}3)\,\,C = \frac{{x + \sqrt x - 2}}{{\sqrt x + 2}}\,\,\,\left( {x \ge 0} \right)\\\,\,\,\,\,\,\,\,\,\,\, = \frac{{x + 2\sqrt x - \sqrt x - 2}}{{\sqrt x + 2}} = \frac{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 1} \right)}}{{\sqrt x + 2}} = \sqrt x - 1.\end{array}\)
Vậy \(C = \sqrt x - 1\) với \(x \ge 0\).
Bài 3
Phương pháp:
1) Thay giá trị của \(x = 49\) (tmđk) vào phương trình để tính.
2) Quy đồng, rút gọn phân thức.
3) Phân tích biểu thức P sao cho hợp lí để có thể sử dụng bất đẳng thức Cô-si cho hai số dương.
Cách giải:
1) Tính giá trị của \(A\) khi \(x = 49\) .
Với \(x = 49\) thỏa mãn điều kiện: \(x \ge 0,x \ne 4\)
Thay \(x = 9\) vào biểu thức \(A\) ta được:
\(A = \frac{{49 - 4}}{{\sqrt {49} - 2}} = \frac{{45}}{{7 - 2}} = \frac{{45}}{5} = 9\).
Vậy \(A = 9\) khi \(x = 49.\)
2) Rút gọn \(B\) .
Điều kiện: \(x \ge 0,\,\,x \ne 4.\)
\(\begin{array}{l}B = \frac{2}{{\sqrt x - 2}} + \frac{3}{{\sqrt x + 2}} - \frac{{x - 5\sqrt x + 2}}{{4 - x}}\\\,\,\,\,\, = \frac{2}{{\sqrt x - 2}} + \frac{3}{{\sqrt x + 2}} + \frac{{x - 5\sqrt x + 2}}{{x - 4}}\,\,\\\,\,\,\,\, = \frac{2}{{\sqrt x - 2}} + \frac{3}{{\sqrt x + 2}} + \frac{{x - 5\sqrt x + 2}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\,\,\,\,\\\,\,\,\,\,\, = \frac{{2\left( {\sqrt x + 2} \right) + 3\left( {\sqrt x - 2} \right) + x - 5\sqrt x + 2}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\,\,\,\,\\\,\,\,\,\,\, = \frac{{2\sqrt x + 4 + 3\sqrt x - 6 + x - 5\sqrt x + 2}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\,\,\,\\\,\,\,\,\, = \frac{x}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\,\,\, = \frac{x}{{x - 4}}\,\,\,.\end{array}\)
Vậy \(B = \frac{x}{{x - 4}}\) với \(x \ge 0;x \ne 4\).
3) Với \(x > 4\) , tìm giá trị nhỏ nhất của biểu thức \(P = A.B\) .
Với \(x > 4\), ta có:
\(\begin{array}{l}P = A.B = \frac{{x - 4}}{{\sqrt x - 2}}.\frac{x}{{x - 4}} = \frac{x}{{\sqrt x - 2}}\\ \Rightarrow P = \frac{{x - 4 + 4}}{{\sqrt x - 2}} = \frac{{x - 4}}{{\sqrt x - 2}} + \frac{4}{{\sqrt x - 2}}\\\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}{{\sqrt x - 2}} + \frac{4}{{\sqrt x - 2}}\\\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt x + 2 + \frac{4}{{\sqrt x - 2}} = \sqrt x - 2 + \frac{4}{{\sqrt x - 2}} + 4\end{array}\)
Khi \(x > 4\) thì \( \Rightarrow \sqrt x > 2 \Rightarrow \left\{ \begin{array}{l}\sqrt x - 2 > 0\\\frac{4}{{\sqrt x - 2}} > 0\end{array} \right.\)
Áp dụng bất đẳng thức Cô-si cho hai số dương \(\sqrt x - 2\,\) và \(\frac{4}{{\sqrt x - 2}}\) ta được:
\(\begin{array}{l}\sqrt x - 2 + \frac{4}{{\sqrt x - 2}} \ge 2.\sqrt {\left( {\sqrt x - 2} \right).\frac{4}{{\sqrt x - 2}}} = 2\sqrt 4 = 4\\ \Rightarrow \sqrt x - 2 + \frac{4}{{\sqrt x - 2}} + 4 \ge 4 + 4 = 8\,\,\,\,\,\,\,hay\,\,\,\,\,\,\,P \ge 8\end{array}\)
Dấu “=” xảy ra \( \Leftrightarrow \sqrt x - 2 = \frac{4}{{\sqrt x - 2}} \Rightarrow {\left( {\sqrt x - 2} \right)^2} = 4\)
\( \Leftrightarrow \left[ \begin{array}{l}\sqrt x - 2 = 2\\\sqrt x - 2 = - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\sqrt x = 4\\\sqrt x = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 16\,\,\,\,\,\left( {tm\,\,\,\,\,x > 4} \right)\\x = 0\,\,\,\,\left( {ktm\,\,\,\,x > 4} \right)\end{array} \right.\)
Vậy giá trị nhỏ nhất của \(P = 8\) khi và chỉ khi \(x = 16\).
Bài 4
Phương pháp:
a) Sử dụng định lý Pitago và tỉ số lượng giác của góc nhọn trong tam giác vuông để làm bài.
b, c) Sử dụng công thức hệ thức lượng trong tam giác vuông để làm bài.
Cách giải:
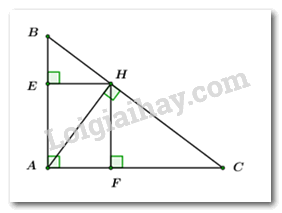
a) Giải \(\Delta ABC.\)
\(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{6^2} - {3^2}} = \sqrt {27} = 3\sqrt 3 \,\,cm.\)Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại\(A\) ta có:
Xét \(\Delta ABC\) vuông tại \(A\) ta có:
\(\begin{array}{l}\cos \angle B = \frac{{AB}}{{BC}} = \frac{3}{6} = \frac{1}{2} \Rightarrow \angle B = {60^0}\\ \Rightarrow \angle C = {90^0} - \angle B = {90^0} - {60^0} = {30^0}.\end{array}\)
b) Tính \(AH\) và chứng minh \(EF = AH.\)
Áp dụng hệ thức lượng cho \(\Delta ABC\) vuông tại\(A\) có đường cao \(AH\) ta có:
\(AH = \frac{{AB.AC}}{{BC}} = \frac{{3.3\sqrt 3 }}{6} = \frac{{3\sqrt 3 }}{2}\,\,cm.\)
Xét tứ giác \(AEHF\) ta có: \(\angle A = \angle E = \angle F = {90^0}\,\,\,\left( {gt} \right)\)
\( \Rightarrow AEHF\) là hình chữ nhật (dhnb).
\( \Rightarrow AH = EF\) (hai đường chéo hình chữ nhật).
c) Tính \(EA.EB + AF.FC.\)
Áp dụng hệ thức lượng cho \(\Delta ABH\) vuông tại \(H\) có đường cao \(HE\) ta có:
\(AH.BC = AB.AC \Rightarrow AH = \frac{{AB.AC}}{{BC}} = \frac{{3.3\sqrt 3 }}{6} = \frac{{3\sqrt 3 }}{2}\,\,cm.\)
Áp dụng hệ thức lượng cho \(\Delta ABH\) vuông tại \(H\) có đường cao \(HE\) ta có:
\(H{E^2} = EA.EB\)
Áp dụng hệ thức lượng cho \(\Delta ACH\) vuông tại \(H\) có đường cao \(HF\) ta có:
\(\begin{array}{l}H{F^2} = AF.FC\\ \Rightarrow EB.EA + AF.DC = H{E^2} + H{F^2} = A{H^2} = {\left( {\frac{{3\sqrt 3 }}{2}} \right)^2} = \frac{{27}}{4}\,.\end{array}\)
Bài 5
Tìm giá trị nhỏ nhất của biểu thức \(A = \frac{1}{{{x^2} + {y^2}}} + \frac{2}{{xy}} + 4xy\) với \(x > 0;y > 0;x + y \le 1\) .
\(A = \frac{1}{{{x^2} + {y^2}}} + \frac{2}{{xy}} + 4xy = \left( {\frac{1}{{{x^2} + {y^2}}} + \frac{1}{{2xy}}} \right) + \frac{5}{{4xy}} + \left( {\frac{1}{{4xy}} + 4xy} \right)\)
Áp dụng bất đẳng thức \(\frac{{a + b}}{2} \ge \sqrt {ab} \) với \(a,\,\,\,b > 0\)
Với \(x > 0;y > 0;x + y \le 1\) , ta có:
\(\frac{1}{{{x^2} + {y^2}}} + \frac{1}{{2xy}} \ge \frac{2}{{\sqrt {\left( {{x^2} + {y^2}} \right).2xy} }} \ge 2.\frac{2}{{{x^2} + {y^2} + 2xy}} = \frac{4}{{{{\left( {x + y} \right)}^2}}} \ge \frac{4}{{{1^2}}} = 4\,\,\,\,\left( {do\,\,\,x + y \le 1} \right).\)
\(\begin{array}{l}\frac{5}{{4xy}} \ge \frac{5}{{{{\left( {x + y} \right)}^2}}} \ge 5\,\,\,\left( {do\,\,\,x + y \le 1} \right)\\\frac{1}{{4xy}} + 4xy \ge 2\sqrt {\frac{1}{{4xy}}.4xy} = 2\\ \Rightarrow A \ge 4 + 5 + 2 = 11.\end{array}\)
Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}x = y\\x + y = 1\end{array} \right. \Rightarrow x = y = \frac{1}{2}\)
Vậy GTNN của \(A\) là \(11\) khi và chỉ khi \(x = y = \frac{1}{2}\).