Đề kiểm tra giữa kì 1 Toán 9 - Đề số 2 có lời giải chi tiết
Đề kiểm tra giữa kì 1 Toán 9 - Đề số 2 có lời giải chi tiết
Đề bài
Câu 1 (2 điểm): Thực hiện phép tính:
a) \(5\sqrt {12} - \sqrt {27} - 2\sqrt {75} + \sqrt {48} \)
b) \(\frac{2}{{\sqrt {13} - \sqrt {11} }} + \frac{5}{{4 + \sqrt {11} }} - \sqrt {52} \)
c) \(\sqrt {6 + 2\sqrt 5 } + \sqrt {9 - 4\sqrt 5 } - \sqrt {20} \)
Câu 2 (2 điểm): Giải các phương trình sau:
a) \(3\sqrt x = \sqrt {16x} - 5\)
b) \(\sqrt {4x - 8} - \sqrt {9x - 18} + 4\sqrt {\frac{{x - 2}}{{25}}} = - 3\)
c) \(x - \sqrt {5x + 4} = 2\)
Câu 3 (2 điểm): Cho biểu thức: \(A = \frac{{\sqrt x - 2}}{{\sqrt x + 1}};\) \(B = \frac{{\sqrt x }}{{\sqrt x + 1}} - \frac{{\sqrt x - 4}}{{1 - x}}\,\,\,\left( {x \ge 0,\,\,x \ne 1} \right).\)
a) Tính giá trị của biểu thức \(A\) khi \(x = 25.\)
b) Rút gọn biểu thức \(B.\)
c) Tìm \(x\)để \(A:B < \frac{1}{2}.\)
Câu 4 (3 điểm): Cho \(\Delta ABC\) vuông tại \(A,\) đường cao \(AH,\) \(AB = 6cm,\) \(BC = 10\,cm.\)
a) Giải tam giác vuông \(ABC.\) ( kết quả làm tròn đến phút )
b) Kẻ tia phân giác góc \(A\) cắt \(BC\) tại \(E.\) Tính \(BE,\,\,AE.\)
c) Gọi \(M,\,\,N\) theo thứ tự là hình chiếu của \(E\) trên \(AB\) và \(AC.\) Tính diện tích tứ giác \(AMEN.\)
Câu 5 (1 điểm):
a) Giải bài toán sau: ( kết quả làm tròn đến số thập phân thứ hai )
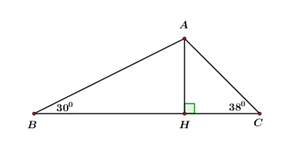
Để đo chiều rộng của một khúc sông \(AH,\) người ta chọn hai vị trí \(B,\,\,C\) cùng một bờ. Biết \(BC = 60\,\,m,\) \(\angle ACB = {38^0},\) \(\angle ABC = {30^0}.\) Hãy tính chiều rộng \(AH\) của khúc sông đó.
b) Tính giá trị nhỏ nhất của biểu thức \(A = \sqrt {{{\left( {x - 2019} \right)}^2}} + \sqrt {{{\left( {x - 2020} \right)}^2}} .\)
Lời giải chi tiết
Câu 1
Phương pháp:
a) Sử dụng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right.,\,\,B \ge 0.\)
b) Sử dụng công thức trục căn thức ở mẫu: \(\frac{1}{{\sqrt A - \sqrt B }} = \frac{{\sqrt A + \sqrt B }}{{A - B}}\,\,\,\left( {A \ge 0,\,\,B \ge 0,\,\,A \ne B} \right)\) và \(\frac{1}{{A + \sqrt B }} = \frac{{A - \sqrt B }}{{{A^2} - B}}\) với \(B \ge 0,\,\,{A^2} \ne B.\)
c) Sử dụng công thức hằng đẳng thức ở mẫu: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,\,A \ge 0\\ - A\,\,\,khi\,\,\,A < 0\end{array} \right..\)
Cách giải:
Thực hiện phép tính:
a) \(5\sqrt {12} - \sqrt {27} - 2\sqrt {75} + \sqrt {48} \)
\(\begin{array}{l} = 5\sqrt {{{3.2}^2}} - \sqrt {{3^2}.3} - 2\sqrt {{5^2}.3} + \sqrt {{4^2}.3} \\ = 5.2\sqrt 3 - 3\sqrt 3 - 2.5\sqrt 3 + 4\sqrt 3 \\ = 10\sqrt 3 - 3\sqrt 3 - 10\sqrt 3 + 4\sqrt 3 \\ = \sqrt 3 .\end{array}\)
b) \(\frac{2}{{\sqrt {13} - \sqrt {11} }} + \frac{5}{{4 + \sqrt {11} }} - \sqrt {52} \)
\(\begin{array}{l} = \frac{{2\left( {\sqrt {13} + \sqrt {11} } \right)}}{{13 - 11}} + \frac{{5\left( {4 - \sqrt {11} } \right)}}{{{4^2} - 11}} - \sqrt {{2^2}.13} \\ = \frac{{2\left( {\sqrt {13} + \sqrt {11} } \right)}}{2} + \frac{{5\left( {4 - \sqrt {11} } \right)}}{5} - \sqrt {{2^2}.13} \\ = \sqrt {13} + \sqrt {11} + 4 - \sqrt {11} - 2\sqrt {13} \\ = 4 - \sqrt {13} .\end{array}\)
c) \(\sqrt {6 + 2\sqrt 5 } + \sqrt {9 - 4\sqrt 5 } - \sqrt {20} \)
\(\begin{array}{l} = \sqrt {{{\left( {\sqrt 5 } \right)}^2} + 2\sqrt 5 + 1} + \sqrt {{{\left( {\sqrt 5 } \right)}^2} - 2.2.\sqrt 5 + {2^2}} - \sqrt {{2^2}.5} \\ = \sqrt {{{\left( {\sqrt 5 + 1} \right)}^2}} + \sqrt {{{\left( {\sqrt 5 - 2} \right)}^2}} - 2\sqrt 5 \\ = \left| {\sqrt 5 + 1} \right| + \left| {\sqrt 5 - 2} \right| - 2\sqrt 5 \\ = \sqrt 5 + 1 + \sqrt 5 - 2 - 2\sqrt 5 \,\,\,\,\left( {do\,\,\,\sqrt 5 - 2 > 0} \right)\\ = - 1.\end{array}\)
Câu 2
Phương pháp:
Tìm điều kiện để phương trình xác định.
Giải phương trình: \(\sqrt {f\left( x \right)} = a\,\,\left( {a \ge 0} \right)\) \( \Leftrightarrow {f^2}\left( x \right) = {a^2}.\)
Cách giải:
Giải các phương trình sau:
a) \(3\sqrt x = \sqrt {16x} - 5\,\,\,\,\left( * \right)\)
Điều kiện: \(x \ge 0\)
\(\begin{array}{l} \Rightarrow \left( * \right) \Leftrightarrow 3\sqrt x = 4\sqrt x - 5\\ \Leftrightarrow \sqrt x = 5 \Leftrightarrow x = 25\,\,\left( {tm} \right)\end{array}\)
Vậy phương trình có nghiệm \(x = 25.\)
b) \(\sqrt {4x - 8} - \sqrt {9x - 18} + 4\sqrt {\frac{{x - 2}}{{25}}} = - 3\,\,\,\,\left( * \right)\)
Điều kiện:\(x \ge 2.\)
\(\begin{array}{l} \Rightarrow \left( * \right) \Leftrightarrow \sqrt {4\left( {x - 2} \right)} - \sqrt {9\left( {x - 2} \right)} + 4.\frac{{\sqrt {x - 2} }}{{\sqrt {25} }} = - 3\\ \Leftrightarrow 2\sqrt {x - 2} - 3\sqrt {x - 2} + \frac{4}{5}\sqrt {x - 2} = - 3\\ \Leftrightarrow - \frac{1}{5}.\sqrt {x - 2} = - 3\\ \Leftrightarrow \sqrt {x - 2} = 15\\ \Leftrightarrow x - 2 = 225\\ \Leftrightarrow x = 227\,\,\left( {tm} \right)\end{array}\)
Vậy phương trình có nghiệm \(x = 227.\)
c) \(x - \sqrt {5x + 4} = 2\,\,\,\left( * \right)\)
Điều kiện: \[x \ge - \frac{4}{5}.\]
\(\begin{array}{l} \Rightarrow \left( * \right) \Leftrightarrow x - 2 = \sqrt {5x + 4} \\ \Leftrightarrow \left\{ \begin{array}{l}x - 2 \ge 0\\{\left( {x - 2} \right)^2} = 5x + 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\{x^2} - 4x + 4 = 5x + 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\{x^2} - 9x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\x\left( {x - 9} \right) = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\\left[ \begin{array}{l}x = 0\\x - 9 = 0\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\\left[ \begin{array}{l}x = 0\\x = 9\end{array} \right.\end{array} \right. \Leftrightarrow x = 9.\end{array}\)
Vậy phương trình có nghiệm \(x = 9.\)
Câu 3
Phương pháp:
a) Thay giá trị \(x = 25\,\,\left( {tm} \right)\) vào biểu thức \(A\) để tính giá trị của biểu thức.
b) Biến đổi, quy đồng sau đó rút gọn biểu thức đã cho.
c) Giải bất phương trình \(A:\,B < \frac{1}{2}\) để tìm \(x.\) Đối chiếu với điều kiện xác định rồi kết luận.
Cách giải:
Cho biểu thức: \(A = \frac{{\sqrt x - 2}}{{\sqrt x + 1}};\) \(B = \frac{{\sqrt x }}{{\sqrt x + 1}} - \frac{{\sqrt x - 4}}{{1 - x}}\,\,\,\left( {x \ge 0,\,\,x \ne 1} \right).\)
a) Tính giá trị của biểu thức \(A\) khi \(x = 25.\)
Điều kiện: \(x \ge 0,\,\,x \ne 1.\)
Thay giá trị \(x = 25\,\,\left( {tm} \right)\) vào biểu thức ta được: \(A = \frac{{\sqrt {25} - 2}}{{\sqrt {25} + 1}} = \frac{{5 - 2}}{{5 + 1}} = \frac{1}{2}.\)
Vậy với \(x = 25\) thì \(A = \frac{1}{2}.\)
b) Rút gọn biểu thức \(B.\)
Điều kiện: \(x \ge 0,\,\,x \ne 1.\)
\(\begin{array}{l}B = \frac{{\sqrt x }}{{\sqrt x + 1}} - \frac{{\sqrt x - 4}}{{1 - x}}\,\,\, = \frac{{\sqrt x }}{{\sqrt x + 1}} + \frac{{\sqrt x - 4}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\\\,\,\,\,\, = \frac{{\sqrt x \left( {\sqrt x - 1} \right) + \sqrt x - 4}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} = \frac{{x - \sqrt x + \sqrt x - 4}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} = \frac{{x - 4}}{{x - 1}}.\end{array}\)
c) Tìm \(x\) để \(A:B < \frac{1}{2}.\)
Điều kiện: \(x \ge 0,\,\,x \ne 1.\)
Ta có: \(A:B < \frac{1}{2}\)
\(\begin{array}{l} \Leftrightarrow \frac{{\sqrt x - 2}}{{\sqrt x + 1}}:\frac{{x - 4}}{{x - 1}} < \frac{1}{2}\\ \Leftrightarrow \frac{{\sqrt x - 2}}{{\sqrt x + 1}}.\frac{{x - 1}}{{x - 4}} < \frac{1}{2}\\ \Leftrightarrow \frac{{\sqrt x - 2}}{{\sqrt x + 1}}.\frac{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} < \frac{1}{2}\\ \Leftrightarrow \frac{{\sqrt x - 1}}{{\sqrt x + 2}} - \frac{1}{2} < 0\\ \Leftrightarrow \frac{{2\sqrt x - 2 - \sqrt x - 2}}{{2\left( {\sqrt x + 2} \right)}} < 0\\ \Leftrightarrow \sqrt x - 4 < 0\,\,\,\left( {do\,\,\,2\left( {\sqrt x + 2} \right) > 0\,\,\forall x\,\,tm\,\,dkxd} \right)\\ \Leftrightarrow \sqrt x < 4\\ \Leftrightarrow x < 16\end{array}\)
Kết hợp với điều kiện \(x \ge 0,\,\,x \ne 1\) ta có: \(0 \le x < 16,\,\,x \ne 1\) thỏa mãn bài toán.
Vậy \(0 \le x < 16,\,\,x \ne 1\) thỏa mãn bài toán.
Câu 4
Phương pháp:
a) Sử dụng định lý Pitago và tỉ số lượng giác của góc nhọn trong tam giác để giải \(\Delta ABC.\)
b) Sử dụng tính chất tia phân giác của tam giác để tính \(BE,\,\,AE.\)
Ta có: \(AE\) là tia phân giác của \(\angle A\) \( \Rightarrow \frac{{BE}}{{BA}} = \frac{{CE}}{{CA}}.\)
c) Chứng minh tứ giác \(AMEN\) là hình chữ nhật.
Vì \(AE\) là phân giác của \(\angle A\) \( \Rightarrow \angle MAE = \angle NEA = {45^0}\)
\( \Rightarrow \Delta AME,\,\,\Delta ANE\) là các tam giác vuông cân tị \(M\) và \(N.\)
\( \Rightarrow AMEN\) là hình vuông.
Từ đó tính \(AM,\,\,AN\) \( \Rightarrow {S_{AMEN}} = A{M^2}.\)
Cách giải:
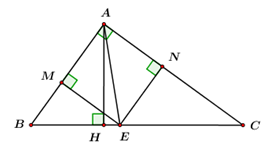
Cho \(\Delta ABC\) vuông tại \(A,\) đường cao \(AH,\) \(AB = 6cm,\) \(BC = 10\,cm.\)
a) Giải tam giác vuông \(ABC.\) (kết quả làm tròn đến phút)
Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) ta có:
\(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{10}^2} - {6^2}} = 8\,\,cm.\)
Xét \(\Delta ABC\) vuông tại \(A\) ta có:
\(\sin \angle B = \frac{{AC}}{{BC}} = \frac{8}{{10}} = \frac{4}{5}\) \( \Rightarrow \angle B \approx {53^0}8'\)
\(\sin \angle C = \frac{{AB}}{{BC}} = \frac{6}{{10}} = \frac{3}{5}\) \( \Rightarrow \angle C \approx {36^0}52'\)
Vậy \(AC = \,8\,\,cm,\,\,\angle B \approx {53^0}8',\,\,\angle C \approx {36^0}52'.\)
b) Kẻ tia phân giác góc \(A\) cắt \(BC\) tại \(E.\) Tính \(BE,\,\,AE.\)
Áp dụng tính chất của tia phân giác ta có: \(\frac{{BE}}{{BA}} = \frac{{CE}}{{CA}} \Leftrightarrow \frac{{BE}}{6} = \frac{{CE}}{8}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\begin{array}{l}\frac{{BE}}{6} = \frac{{CE}}{8} = \frac{{BE + CE}}{{6 + 8}} = \frac{{10}}{{14}} = \frac{5}{7}\\ \Rightarrow \left\{ \begin{array}{l}BE = \frac{5}{7}.6 = \frac{{30}}{7}\,\,cm\\CE = \frac{5}{7}.8 = \frac{{40}}{7}\,\,cm\end{array} \right..\end{array}\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại\(A,\) có đường cao \(AH\) ta có:
\(AH = \frac{{AB.AC}}{{BC}} = \frac{{6.8}}{{10}} = 4,8\,\,cm.\)
\(A{B^2} = BH.BC\) \( \Rightarrow BH = \frac{{A{B^2}}}{{BC}} = \frac{{{6^2}}}{{10}} = 3,6\,\,cm.\)
\( \Rightarrow HE = BE - BH = \frac{{30}}{7} - 3,6 = \frac{{24}}{{35}}.\)
Áp dụng định lý Pitago cho \(\Delta AHE\) vuông tại \(H\) ta có:
\(AE = \sqrt {A{H^2} + H{E^2}} = \sqrt {4,{8^2} + {{\left( {\frac{{24}}{{35}}} \right)}^2}} \) \( = \sqrt {\frac{{1152}}{{49}}} = \frac{{24\sqrt 2 }}{7}\,\,cm.\)
Vậy \(BE = \frac{{30}}{7}\,\,cm,\,\,\,AE = \frac{{24\sqrt 2 }}{7}\,\,cm.\)
c) Gọi \(M,\,\,N\) theo thứ tự là hình chiếu của \(E\) trên \(AB\) và \(AC.\) Tính diện tích tứ giác \(AMEN.\)
Ta có: \(\left\{ \begin{array}{l}EM \bot AB = \left\{ M \right\}\\EN \bot AC = \left\{ N \right\}\end{array} \right.\) \( \Rightarrow \angle AME = \angle ANE = {90^0}\)
Xét tứ giác \(AMEN\) ta có:\(\angle MAN = \angle AME = \angle ANE = {90^0}\)
\( \Rightarrow AMEN\) là hình chữ nhật.
Vì \(AE\) là phân giác của \(\angle A\) \( \Rightarrow \angle MAE = \angle NEA = {45^0}\)
\( \Rightarrow \Delta AME,\,\,\Delta ANE\) là các tam giác vuông cân tị \(M\) và \(N.\)
\( \Rightarrow AMEN\) là hình vuông.
Xét \(\Delta AME\) vuông cân tại\(M\) ta có:
\(\begin{array}{l}A{E^2} = A{M^2} + M{E^2} = 2A{M^2}\\ \Rightarrow A{M^2} = \frac{{A{E^2}}}{2} = \frac{{1152}}{{2.49}} = \frac{{576}}{{49}}\\ \Rightarrow {S_{AMEN}} = A{M^2} = \frac{{576}}{{49}}\,\,\,c{m^2}.\end{array}\)
Câu 5
Phương pháp:
a) Áp dụng hệ số về cạnh và góc trong các tam giác \(ABH,\,\,ACH\) vuông tại \(H\) để tính \(AH.\)
b) Sử dụng bất đẳng thức trị tuyệt đối: \(\left| a \right| + \left| b \right| \ge \left| {a + b} \right|.\)
Dấu “=” xảy ra \(ab \ge 0.\)
Cách giải:
a) Giải bài toán sau: (kết quả làm tròn đến số thập phân thứ hai)
Để đo chiều rộng của một khúc sông \(AH,\) người ta chọn hai vị trí \(B,\,\,C\) cùng một bờ. Biết \(BC = 60\,\,m,\) \(\angle ACB = {38^0},\) \(\angle ABC = {30^0}.\) Hãy tính chiều rộng \(AH\) của khúc sông đó.

Xét \(\Delta ABH\) vuông tại \(H\) ta có:
Xét \(\Delta ACH\) vuông tại \(H\) ta có: \(CH = AH\cot C = AH\cot {38^0} \approx 1,28AH\)
\(\begin{array}{l} \Rightarrow BC = BH + HC = \sqrt 3 AH + 1,28AH\\ \Leftrightarrow 60 = 3,01AH\\ \Leftrightarrow AH \approx 19,92\,\,m.\end{array}\)
Vậy chiều rộng của khúc sông khoảng \(19,92\,\,m.\)
b) Tính giá trị nhỏ nhất của biểu thức \(A = \sqrt {{{\left( {x - 2019} \right)}^2}} + \sqrt {{{\left( {x - 2020} \right)}^2}} .\)
Ta có:
\(\begin{array}{l}A = \sqrt {{{\left( {x - 2019} \right)}^2}} + \sqrt {{{\left( {x - 2020} \right)}^2}} \\\,\,\,\,\, = \left| {x - 2019} \right| + \left| {x - 2020} \right|\\\,\,\,\,\, = \left| {x - 2019} \right| + \left| {2020 - x} \right|\\\,\,\,\,\, \ge \left| {x - 2019 + 2020 - x} \right| = 1\end{array}\)
Dấu “=” xảy ra \( \Leftrightarrow \left( {x - 2019} \right)\left( {2020 - x} \right) \ge 0\)
\(\begin{array}{l} \Leftrightarrow \left( {x - 2019} \right)\left( {x - 2020} \right) \le 0\\ \Leftrightarrow 2019 \le x \le 2020.\end{array}\)
Vậy \(MinA = 1\) khi \(2019 \le x \le 2020.\)