Đề kiểm tra 45 phút - Đề số 5 - Chương 1 - Hình học 9
Giải Đề kiểm tra 45 phút - Đề số 5 - Chương 1 - Hình học 9
Đề bài
Bài 1. Tính :
a. \(\left( {\cos 36^\circ - \sin 36^\circ } \right).\left( {\cos 37^\circ - \sin 38^\circ } \right).\left( {\cos 42^\circ - \sin 48^\circ } \right)\)
b. \(\left( {\tan 52^\circ + \cot 43^\circ } \right).\left( {\tan 29^\circ - \cot 61^\circ } \right).\left( {\tan 13^\circ - \tan 24^\circ } \right)\)
Bài 2. Cho tam giác ABC vuông tại A có \(AB = 6cm, BC = 10cm\), đường cao AH. Gọi E, F là hình chiếu của H lần lượt lên AB, AC.
a. Tính EF
b. Chứng minh rằng : \(AE.AB = AF.AC\)
c. Tính : \(A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C\)
Bài 3. Cho tam giác ABC vuông tại A. Từ trung điểm E của cạnh AC, vẽ EF vuông góc với BC.
a. Chứng minh rằng : \(AF = BE.\cos C\).
b. Cho \(BC = 20cm; \sin C = 0,6\). Tính \({S_{AEFB}}\)
LG bài 1
Phương pháp giải:
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia
Lời giải chi tiết:
a. Ta có: \(\cos 42^\circ = \sin 48^\circ \) (vì là hai góc phụ nhau)
\(⇒ \cos42^o - \sin48^o = 0\)
Do đó: \(\left( {\cos 36^\circ - \sin 36^\circ } \right).\left( {\cos 37^\circ - \sin 38^\circ } \right).\left( {\cos 42^\circ - \sin 48^\circ } \right) = 0\)
b. Ta có: \(\tan 29^\circ = \cot 61^\circ \)\(\;\Rightarrow \tan 29^\circ - \cot 61^\circ = 0\)
Do đó: \(\left( {\tan 52^\circ + \cot 43^\circ } \right).\left( {\tan 29^\circ - \cot 61^\circ } \right).\left( {\tan 13^\circ - \tan 24^\circ } \right) = 0\)
LG bài 2
Phương pháp giải:
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Khi đó ta có các hệ thức sau:
+) \(A{B^2} = BH.BC\) và \(A{C^2} = CH.BC\)
+) \(H{A^2} = HB.HC\)
+) \(AB.AC = BC.AH\)
+) \(B{C^2} = A{B^2} + A{C^2}\) (Định lí Pitago).
+) \(\sin B = \dfrac{{AC}}{{BC}};\cos B = \dfrac{{AB}}{{BC}}\)
Lời giải chi tiết:
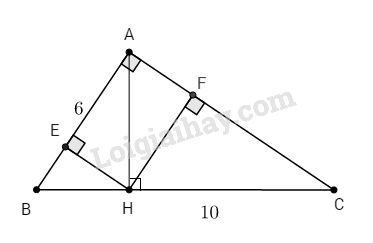
a. Ta có: \(∆ABC\) vuông tại A:
\(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{10}^2} - {6^2}} = 8\,\left( {cm} \right)\)
Lại có AH là đường cao của tam giác vuông ABC nên:
\(AH.BC = AB.AC\) (định lí 3)
\( \Rightarrow AH = {{AB.AC} \over {BC}} = {{6.8} \over {10}} = 4,8\,\left( {cm} \right)\)
Lại có tứ giác AFHE là hình chữ nhật (vì có ba góc vuông) nên \(EF = AH = 4,8 \;(cm)\)
b. Xét tam giác vuông AHB có đường cao HE, ta có:
\(A{H^2} = AE.AB\) (định lí 1) (1)
Xét tam giác vuông AHC có đường cao HF, ta có:
\(A{H^2} = AF.AC\) (2)
Từ (1) và (2) suy ra: \(AE.AB = AF.AC\)
c. Ta có:
\(\eqalign{ & \sin B = {{AC} \over {BC}} \Rightarrow {\sin ^2}B = {{A{C^2}} \over {B{C^2}}} \cr & \sin C = {{AB} \over {BC}} \Rightarrow {\sin ^2}C = {{A{B^2}} \over {B{C^2}}} \cr & \tan B = {{AC} \over {AB}} \Rightarrow \tan C = {{AB} \over {AC}} \cr} \)
Vậy \(\eqalign{ A &= {\sin ^2}B + {\sin ^2}C - \tan B.\tan C \cr & = {{A{C^2}} \over {B{C^2}}} + {{A{B^2}} \over {B{C^2}}} - {{AC} \over {AB}}.{{AB} \over {AC}} \cr&= {{A{C^2} + A{B^2}} \over {B{C^2}}} - 1 \cr} \)
\(\;\;\;\;\; = {{B{C^2}} \over {B{C^2}}} - 1\) (định lí Pi-ta-go)
\(\;\;\;\;\;=1 – 1 = 0\)
LG bài 3
Phương pháp giải:
Sử dụng tính chất tam giác đồng dạng và định lý Pytago
Lời giải chi tiết:
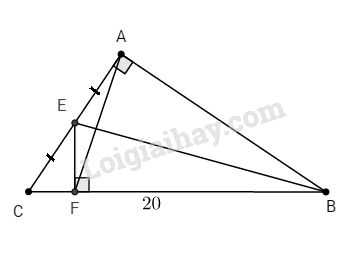
a. Ta có: ∆BAC đồng dạng ∆EFC (g.g) \( \Rightarrow {{AC} \over {BC}} = {{FC} \over {EC}}\) (1)
Xét ∆AFC và ∆BEC có \(\widehat C\) chung và (1)
Do đó ∆AFC đồng dạng ∆BEC (c.g.c)
\(\eqalign{ & \Rightarrow {{AF} \over {BE}} = {{AC} \over {BC}} = \cos C \cr & \Rightarrow AF = BE.\cos C\,\left( {dpcm} \right) \cr} \)
b. Ta có: \({S_{AEFB}} = {S_{ABC}} - {S_{EFC}}\)
Ta có: \(\sin C = 0,6 \Rightarrow \widehat C \approx 36^\circ 52'\)
∆ABC vuông tại A nên \(AB = BC.sinC = 20.0,6 = 12\; (cm)\)
Tương tự: \(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{20}^2} - {{12}^2}} = 16\,\left( {cm} \right)\)
Do đó: \({S_{ABC}} = {1 \over 2}AB.AC = {1 \over 2}12.16 = 96\,\left( {c{m^2}} \right)\)
∆BAC và ∆EFC đồng dạng (cmt), ta có:
\(\eqalign{ & {{{S_{EFC}}} \over {{S_{BAC}}}} = {\left( {{{EC} \over {BC}}} \right)^2} = {\left( {{8 \over {20}}} \right)^2} = {{64} \over {400}} \cr & \Rightarrow {S_{EFC}} = {{{S_{ABC}}.64} \over {400}} = {{96.64} \over {400}} \approx 15,36\,\left( {c{m^2}} \right) \cr & \text{Vậy }\,{S_{AEFB}} = 96 - 15,36 = 80,64\,\left( {c{m^2}} \right) \cr} \)