Đề kiểm tra 45 phút - Đề số 2 - Chương 1 - Hình học 9
Giải Đề kiểm tra 45 phút - Đề số 2 - Chương 1 - Hình học 9
Đề bài
Bài 1. Cho góc nhọn α, biết \(\cos \alpha = {3 \over 4}\). Không tính số đo góc \(α\), hãy tính \(\sinα, \tanα, \cotα\).
Bài 2. Cho \(∆ABC\) có \(AB = 12cm, AC = 16cm, \)\(BC = 20cm.\)
a. Tính đường cao AH của ∆ABC
b. Chứng minh rằng: \(AB.\cos B + AC.\cos C = 20cm\)
Bài 3. Cho hình bình hành \(ABCD\) có AC là đường chéo lớn. Kẻ \(CH ⊥ AD (H ∈ AD)\) và \(CK ⊥ AB (K ∈ AB)\)
a. Chứng minh : \(∆CKH\) và \(∆ABC\) đồng dạng.
b. Chứng minh: \(HK = AC.\sin \widehat {BAD}\)
LG bài 1
Phương pháp giải:
Sử dụng:
\(\begin{array}{l} {\sin ^2}\alpha + {\cos ^2}\alpha = 1\\ \tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\\ \cot \alpha .\tan \alpha = 1 \end{array}\)
Lời giải chi tiết:
Ta có:
\(\eqalign{ & {\sin ^2}\alpha + {\cos ^2}\alpha = 1 \cr&\Rightarrow \sin \alpha = \sqrt {1 - {{\cos }^2}\alpha }\cr&\;\;\;\;\;\;\;\;\;\;\;\;\; = \sqrt {1 - {{\left( {{3 \over 4}} \right)}^2}} = {{\sqrt 7 } \over 4} \cr & \tan \alpha = {{\sin \alpha } \over {\cos \alpha }} = {{\sqrt 7 } \over 4}:{3 \over 4} = {{\sqrt 7 } \over 3};\,\cr&\cot \alpha = \frac{1}{{\tan \alpha }}= {{3\sqrt 7 } \over 7} \cr} \)
Cách khác:
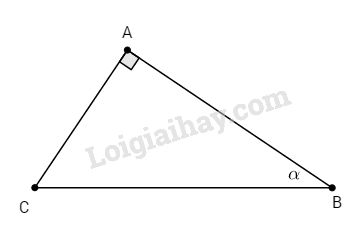
Xét \(∆ABC\) vuông tại A, có các kích thước như hình vẽ bên; \(\widehat {ABC} = \alpha \)
\(\eqalign{ & \cos \alpha = {3 \over 4}\,hay\,{c \over a} = {3 \over 4} \cr & \Rightarrow c = {3 \over 4}a \Rightarrow {c^2} = {9 \over {16}}{a^2} \cr} \)
Theo định lí Pi-ta-go, ta có:
\(\eqalign{ & {b^2} = {a^2} - {c^2} = {a^2} - {9 \over {16}}{a^2} = {7 \over {16}}{a^2}\cr& \Rightarrow b = {{\sqrt 7 } \over 4}a \cr & \Rightarrow \sin \alpha = {b \over a} = {{\sqrt 7 } \over 4};\,\tan \alpha = {{\sqrt 7 } \over 3};\cr&\cot \alpha = {{3\sqrt 7 } \over 7} \cr} \)
LG bài 2
Phương pháp giải:
Sử dụng hệ thức lượng trong tam giác vuông và tỉ số lượng giác của góc nhọn.
Lời giải chi tiết:
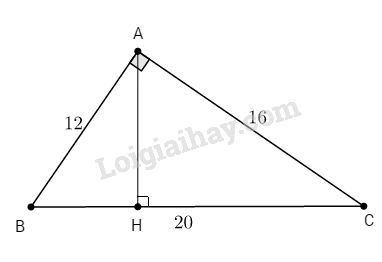
a. Dễ thấy \(∆ABC\) vuông tại A vì:
\(A{B^2} + A{C^2} = B{C^2}\left( {{{12}^2} + {{16}^2} = {{20}^2}} \right)\) (định lí Pi-ta-go đảo)
Xét \(∆ABC\) vuông, đường cao AH, ta có:
\(AH.BC = AB.AC\) (định lí 3)
\( \Rightarrow AH = {{AB.AC} \over {BC}} = {{12.16} \over {20}} = 9,6\,\left( {cm} \right)\)
b. Ta có: \(\cos B = {{AB} \over {BC}};\,\cos C = {{AC} \over {BC}}\)
Biến đổi vế trái :
\(\eqalign{ & AB.\cos B + AC.\cos C \cr&= AB.{{AB} \over {BC}} + AC.{{AC} \over {BC}} \cr&= {{A{B^2}} \over {BC}} + {{A{C^2}} \over {BC}} \cr & = {{A{B^2} + A{C^2}} \over {BC}} = {{B{C^2}} \over {BC}} = BC \cr} \)
LG bài 3
Phương pháp giải:
Sử dụng tính chất hai tam giác đồng dạng và tỉ số lượng giác của góc nhọn.
Lời giải chi tiết:
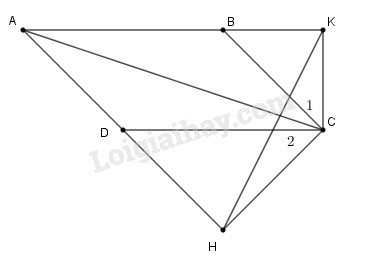
a. Ta có: AB // CD (gt) \( \Rightarrow \widehat {BAD} = \widehat {CDH}\) (đồng vị)
Tương tự : AD // BC \( \Rightarrow \widehat {BAD} = \widehat {KBC}\)
Do đó: \(\widehat {KBC} = \widehat {CDH} \Rightarrow {\widehat C_1} = {\widehat C_2}\)
Vậy \(∆CKB\) đồng dạng \(∆CHD\) (g.g)
\(\eqalign{ & \Rightarrow {{CK} \over {CH}} = {{CB} \over {CD}},\text{ mà }\,CD = AB \cr & \Rightarrow {{CK} \over {CH}} = {{CB} \over {AB}}\,\left( 1 \right) \cr} \)
AB // CD, mà \(AK ⊥ CK ⇒ CD ⊥ CK\) hay \(\widehat {KCD} = \widehat {BKC} = 90^\circ \)
Mặt khác \(\widehat {ABC}\) là góc ngoài của ∆BKC nên:
\(\widehat {ABC} = \widehat {BKC} + {\widehat C_1} = 90^\circ + {\widehat C_1}\)
Lại có: \(\widehat {KCH} = \widehat {KCD} + {\widehat C_2} = 90^\circ + {\widehat C_2}\)
mà \({\widehat C_2} = {\widehat C_1}\,\left( {cmt} \right) \Rightarrow \widehat {ABC} = \widehat {KCH}\) (2)
Từ (1) và (2) \(⇒ ∆CKH\) đồng dạng \(∆BCA\) (c.g.c)
b. Ta có: \(∆CKH\) đồng dạng \(∆BCA\) (cmt)
\(\eqalign{ & \Rightarrow {{HK} \over {CA}} = {{CK} \over {CB}} = \sin \widehat {KBC}\cr& \Rightarrow HK = CA.\sin \widehat {KBC} \cr & \text{Mà }\,\widehat {KBC} = \widehat {BAD}\,\left( {cmt} \right) \cr} \)
Do đó: \(HK = AC.\sin \widehat {BAD}\)