Đề kiểm tra 45 phút (1 tiết) - Đề số 8 - Chương 2 - Hình học 9 — Không quảng cáo

Đề bài

Cho đường tròn (O; 5cm) và (O’; 3cm) tiếp xúc ngoài nhau tại A. Một đường thẳng qua A hợp với OO’ một góc 30˚ cắt (O) tại B và (O’) tại C

a. Chứng minh : \(\widehat {AOB} = \widehat {AO'C}\) và OB // O’C.

b. Chứng minh tiếp tuyến của (O) tại B và tiếp tuyến của (O’) tại C song song với nhau.

c. Tiếp tuyến của (O’) tại C cắt OO’ tại D. Tính CD và O’D

d. DC cắt BO tại E. Tính \({S_{ABE}}\)

Lời giải chi tiết

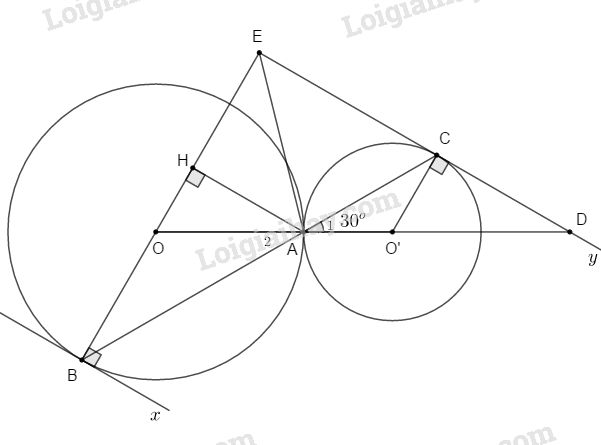
a. Ta có các tam giác AOB và CO’A cân \( \Rightarrow {\widehat A_1} = {\widehat A_2} = \widehat B = \widehat C = 30^\circ \)

\( \Rightarrow \widehat {AOB} = \widehat {AO'C} = 180^\circ  - 2.30^\circ\)\(\,  = 120^\circ \)

Do đó OB // O’C (cặp góc so le trong bằng nhau)

b. \(Bx ⊥ OB, Cy ⊥ O’C\), mà \(OB // O’C ⇒ Bx // Cy\)

c. Ta có: \(\widehat {CO'D} = 60^\circ \) (kề bù với \(\widehat {AO'C} = 120^\circ \) )

Do đó ∆O’CD là nửa tam giác đều mà \(O’C = 3cm\) (gt) \(⇒ O’D = 6cm.\)

Theo định lí Pi-ta-go :

\(CD = \sqrt {O'{D^2} - O'{C^2}}  = \sqrt {{6^2} - {3^2}}  \)\(\,= \sqrt {27}  = 3\sqrt 3 \,\left( {cm} \right)\)

d. Ta có: \(OD = OO’ + O’D = 5 + 3 + 6 = 14\) (cm)

Xét tam giác OED có \(\widehat {EDO} = 30^\circ \,\left( {\text{vì }\widehat {CO'D} = 60^\circ } \right),\)

\(\widehat {EOD} = 60^\circ \) (kề bù với \(\widehat {BOA} = 120^\circ \)) nên ∆OED vuông tại E.

Khi đó \(OE = {1 \over 2}OD = 7cm.\) Do đó \(EB = OE + OB = 7 + 5 = 12\) (cm).

Kẻ đường cao AH của ∆BAE, ta có ∆AHO là nửa tam giác đều có

\(\eqalign{  & OA = 5cm \Rightarrow OH = {5 \over 2}\left( {cm} \right)  \cr  &  \Rightarrow AH = \sqrt {O{A^2} - O{H^2}}  \cr&\;\;\;\;\;\;\;\;\;\;\;\;= \sqrt {{5^2} - {{\left( {{5 \over 2}} \right)}^2}}  = {{5\sqrt 3 } \over 2}({cm}) \cr} \)

Vậy : \({S_{ABE}} = {1 \over 2}BE.AH \)\(\,= {1 \over 2}.12.{{5\sqrt 3 } \over 2} \)\(\,= 15\sqrt 3 \left( {c{m^2}} \right)\)