Đề kiểm tra 45 phút (1 tiết) - Đề số 7 - Chương 2 - Hình học 9
Giải Đề kiểm tra 45 phút (1 tiết) - Đề số 7 - Chương 2 - Hình học 9
Đề bài
Cho ∆ABC vuông tại A. Vẽ đường tròn (O) qua A và tiếp xúc với BC tại B. Vẽ đường tròn (O’) qua A và tiếp xúc với BC tại C.
a. Chứng minh rằng (O) và (O’) tiếp xúc nhau tại A.
b. Gọi I là trung điểm của BC. Chứng minh rằng : \(\widehat {OIO'} = 90^\circ \) và \(AI ⊥ OO’\).
c. Tính các cạnh của ∆ABC biết bán kính của hai đường tròn là R và R’.
Phương pháp giải - Xem chi tiết
a. Ta chứng minh góc OAO' bằng 180 độ từ đó suy ra ba điểm O,A,O' thẳng hàng
b. Sử dụng:
-Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền
-Hai đường phân giác của hai góc kề bù vuông góc với nhau
c.Sử dụng
Hệ thức về cạnh và đường cao trong tam giác vuông
Lời giải chi tiết
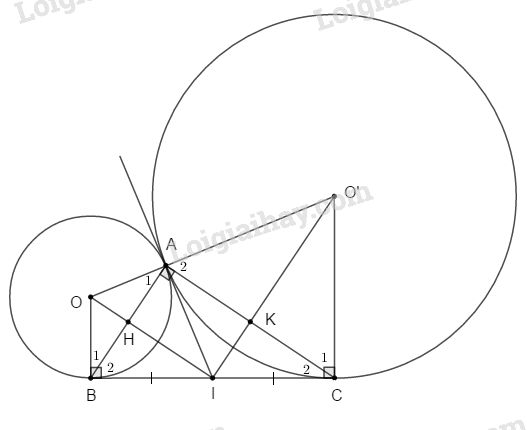
a. (O) và (O’) tiếp xúc với BC tại B và C nên \(OB ⊥ BC\) và \(O’C ⊥ BC\)
hay \({\widehat B_1} + {\widehat B_2} + {\widehat C_1} + {\widehat C_2} = 180^\circ ,\)
mà \({\widehat B_2} + {\widehat C_2} = 90^\circ \) (do ∆ABC vuông tại A) \( \Rightarrow {\widehat B_1} + {\widehat C_1} = 90^\circ \)
∆BOA và ∆CO’A cân tại O và O’ nên.
\(\eqalign{ & {\widehat B_1} = {\widehat A_1},{\widehat C_1} = {\widehat A_2} \cr & \Rightarrow {\widehat A_1} + {\widehat A_2} = 90^\circ \cr} \)
Do đó \({\widehat A_1} + \widehat {BAC} + {\widehat A_2} = 180^\circ \)
Vậy ba điểm O, A, O’ thẳng hàng.
Mặt khác : \(OO’ = OA + AO’\)
nên (O) và (O’) tiếp xúc nhau tại A.
b. I là trung điểm của BC (gt) nên AI là trung tuyến của ∆ABC vuông tại A \(⇒ IA = IB = IC.\)
Do đó \(∆IAO = ∆IBO\) (c.c.c) \( \Rightarrow \widehat {IAO} = \widehat {IBO} = 90^\circ \)
⇒ AI là tiếp tuyến của (O) và (O’). Do đó IO và IO’ là phân giác của các góc kề bù AIB và AIC \( \Rightarrow \widehat {OIO'} = 90^\circ \)
Cách khác : Ta có: \(IA = IB, OA = OB ⇒ OI\) là trung trực của AB
\(⇒ OI ⊥ AB\) hay \(\widehat {AHI} = 90^\circ \) (H là giao điểm của OI và AB).
Chứng minh tương tự có \(\widehat {AKI} = 90^\circ \) (K là giao điểm của O’I và AC) nên AHIK là hình chữ nhật \( \Rightarrow \widehat {OIO'} = 90^\circ \)
c. ∆OIO’ vuông có AI là đường cao ta có:
\(A{I^2} = AO.AO' \Rightarrow AI = \sqrt {R.R'} \). Do đó: \(BC = 2\sqrt {R.R'} \)
Gọi H là giao điểm của OI và AB. ∆OAI vuông tại A (cmt) có AH là đường cao, ta có:
\({1 \over {A{H^2}}} = {1 \over {A{O^2}}} + {1 \over {A{I^2}}}\) (định lí 4)
hay
\(\eqalign{ & {1 \over {A{H^2}}} = {1 \over {{R^2}}} + {1 \over {{{\left( {\sqrt {R.R'} } \right)}^2}}} \cr&\;\;\;\;\;\;\;\;\;\;= {1 \over {{R^2}}} + {1 \over {R.R'}} = {{R' + R} \over {{R^2}R'}} \cr & \Rightarrow AH = R\sqrt {{{R'} \over {R + R'}}} \cr& \Rightarrow AB = 2AH = 2R\sqrt {{{R'} \over {R + R'}}} \cr} \)
Tương tự \(AC = 2R'\sqrt {{R \over {R + R'}}} \)