Đề kiểm tra học kì 2 Toán 10 - Đề số 2 - Chân trời sáng tạo
I. PHẦN TRẮC NGHIỆM ( 35 câu - 7,0 điểm ).
Đề bài
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm ).
Câu 1: Tập xác định của hàm số \(y = \sqrt {x - 6} \) là
A. \(( - \infty ;6{\rm{]}}.\)
B. \([6; + \infty ).\)
C. \((6; + \infty ).\)
D. \(( - \infty ;6).\)
Câu 2: Cho đồ thị của hàm số bậc hai như hình vẽ, trục đối xứng của đồ thị là
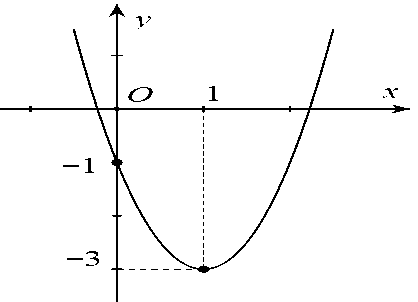
A . \(x = 1.\)
B. \(y = 1.\)
C. \(y = 0.\)
D. \(x = 0.\)
Câu 3: Tìm khẳng định đúng trong các khẳng định sau?
A. \(f\left( x \right) = 3{x^2} + 2x - 5\)là tam thức bậc hai.
B. \(f\left( x \right) = 2x - 4\)là tam thức bậc hai.
C. \(f\left( x \right) = 3{x^3} + 2x - 1\) là tam thức bậc hai.
D. \(f\left( x \right) = {x^4} - {x^2} + 1\) là tam thức bậc hai.
Câu 4: Nghiệm của phương trình \(\sqrt {3x + 5} = 2\) là
A. \(x = - 1\).
B. \(x = 0\).
C. \(x = 4\).
D. \(x = - \frac{1}{3}\).
Câu 5: Cho đường thẳng \(d:x - y + 3 = 0.\) Một vectơ pháp tuyến của \(d\) là
A. \(\overrightarrow n = (1;1).\)
B. \(\overrightarrow x = (1; - 3).\)
C. \(\overrightarrow e = ( - 1; - 1).\)
D. \(\overrightarrow a = (1; - 1).\)
Câu 6: Một vectơ chỉ phương của đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 5 - t\\y = 3 +3t\end{array} \right.\) là
A. \(\overrightarrow x = (3;1).\)
B. \(\overrightarrow e = (5;3).\)
C. \(\overrightarrow a = (3; - 5).\)
D. \(\overrightarrow u = ( - 1;3).\)
Câu 7: Xét vị trí tương đối của hai đường thẳng \({d_1}:x - 2y + 1 = 0\) và \({d_2}: - 3x + 6y - 10 = 0\).
A. Trùngnhau.
B. Song song.
C. Vuôn góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau.
Câu 8: Khoảng cách từ điểm \(M\left( { - 1; - 1} \right)\) đến dường thẳng \(\Delta :4x + 3y - 18 = 0\)
bằng
A. \( - 5.\)
B. \(\frac{7}{5}.\)
C. \( - \frac{7}{5}.\)
D. \(5.\)
Câu 9: Phương trình nào sau đây là phương trình đường tròn?
A. \({x^2} + {y^2} - x - y + 9 = 0\).
B. \({x^2} + {y^2} - x = 0\).
C. \({x^2} + {y^2} - 2xy - 1 = 0.\)
D. \({x^2} - {y^2} - 2x + 3y - 1 = 0.\)
Câu 10: Đường tròn \({(x - 2)^2} + {(y - 1)^2} = 4\) có bán kính là
A. \(4.\)
B. \(2.\)
C. \(16.\)
D. \(1\).
Câu 11: Trong mặt phẳng \(Oxy\), phương trình nào sau đây là phương trình chính tắc của một elip?
A. \(\frac{{{x^2}}}{2} + \frac{{{y^2}}}{3} = - 1\).
B. \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{8} = 1\).
C. \(\frac{x}{9} + \frac{y}{8} = 1\).
D. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{1} = 1\).
Câu 12: Có bao nhiêu cách chọn 1 viên bi trong chiếc hộp có 5 viên bi màu đỏ và 3 viên bi màu vàng?
A. \(8\).
B. \(15\).
C. \(6\).
D. \(4\).
Câu 13: Có \(10\) cái bút khác nhau và \(8\)quyển sách giáo khoa khác nhau. Một bạn học sinh cần chọn \(1\) cái bút và \(1\) quyển sách. Hỏi bạn học sinh đó có bao nhiêu cách chọn?
A. \(80\).
B. \(60\).
C. \(90\).
D. \(70\).
Câu 14: Có bao nhiêu cách sắp xếp \(5\) học sinh thành một hàng dọc?
A. \({5^5}.\).
B. \(5!\).
C. \(4!\).
D. \(5\).
Câu 15: Công thức tính số tổ hợp chập k của n phần tử là
A. \(C_n^k = \frac{{n!}}{{\left( {n - k} \right)!}}\).
B. \(C_n^k = \frac{{n!}}{{\left( {n - k} \right)!k!}}\).
C. \(A_n^k = \frac{{n!}}{{\left( {n - k} \right)!}}\).
D. \(A_n^k = \frac{{n!}}{{\left( {n - k} \right)!k!}}\).
Câu 16: Số cách chọn ra \(3\)học sinh trong \(10\) học sinh bất kì là
A. \(120\).
B. \(6\).
C. \(30\).
D. \(720\).
Câu 17: Trong khai triển nhị thức Niu-tơn của \({\left( {a + b} \right)^4}\) có bao nhiêu số hạng?
A. \(6\).
B. \(3\).
C. \(5\).
D. \(4\).
Câu 18: Gieo một con xúc sắc cân đối đồng chất hai lần. Số phần tử của không gian mẫu là
A. \(9\).
B. \(18\).
C. \(12\).
D. \(36\).
Câu 19: Lấy ngẫu nhiên một thẻ từ một chiếc hộp chứa \(20\) thẻ được đánh số từ \(1\) đến \(20\). Số phần tử của không gian mẫu là
A. \(n\left( \Omega \right) = 20\) .
B. \(n\left( \Omega \right) = 1\).
C. \(n\left( \Omega \right) = 10\).
D. \(n\left( \Omega \right) = 15\).
Câu 20: Rút ngẫu nhiên cùng lúc ba con bài từ cỗ bài tú lơ khơ \(52\) con thì \(n\left( \Omega \right)\) bằng bao nhiêu?
A. \(140608\).
B. \(156\).
C. \(132600\).
D. \(22100\).
Câu 21: Tập giá trị của hàm số \(y = \sqrt {x + 1} \) là:
A. \(( - \infty ;0{\rm{]}}.\)
B. \([0; + \infty ).\)
C. \((1; + \infty ).\)
D. \(\left[ { - 1; + \infty } \right).\)
Câu 22: Hàm số nào sau đây có đồ thị như hình dưới đây?
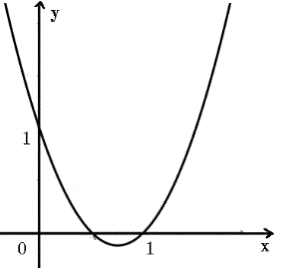
A. \(y = {x^2} - 3x + 1\).
B. \(y = - {x^2} + 3x - 1\).
C. \(y = - 2{x^2} + 3x - 1\).
D. \(y = 2{x^2} - 3x + 1\).
Câu 23: Cho tam thức bậc hai \(f\left( x \right) = - 2{x^2} + 8x - 8\). Trong các mệnh đề sau, mệnh đề nào đúng?
A. \(f\left( x \right) < 0\) với mọi\(x \in \mathbb{R}\).
B. \(f\left( x \right) \ge 0\) với mọi\(x \in \mathbb{R}\).
C. \(f\left( x \right) \le 0\) với mọi\(x \in \mathbb{R}\).
D. \(f\left( x \right) > 0\) với mọi\(x \in \mathbb{R}\).
Câu 24: Phương trình \(\sqrt { - {x^2} + 4x} = 2x - 2\) có bao nhiêu nghiệm?
A. \(3\).
B. \(0\).
C. \(2\).
D. \(1\).
Câu 25: Phương trình tham số của đường thẳng qua \(M\left( {1; - 1} \right)\), \(N\left( {4;3} \right)\) là
A. \(\left\{ \begin{array}{l}x = 3 + t\\y = 4 - t\end{array}\right.\).
B. \(\left\{ \begin{array}{l}x = 1 + 3t\\y = 1 + 4t\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x = 3 - 3t\\y = 4 - 3t\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x = 1 + 3t\\y = - 1 + 4t\end{array} \right.\).
Câu 26: Góc giữa hai đường thẳng \(a:\,\sqrt 3 x - y + 7 = 0\) và \(b:x - \sqrt 3 y - 1 = 0\) là
A. \(30^\circ \).
B. \(90^\circ \).
C. \(60^\circ \).
D. \(45^\circ \).
Câu 27: Đường tròn tâm \(I( - 1;2)\) và đi qua điểm \(M(2;1)\) có phương trình là
A. \({x^2} + {y^2} + 2x - 4y - 5 = 0\).
B. \({x^2} + {y^2} + 2x - 4y - 3 = 0.\)
C. \({x^2} + {y^2} - 2x - 4y - 5 = 0\).
D. \({x^2} + {y^2} + 2x + 4y - 5 = 0.\)
Câu 28: Đường tròn đi qua \(3\) điểm \(A\left( {0;2} \right),{\rm{ }}B\left( {2;2} \right),{\rm{ }}C(1;1 + \sqrt2 )\)có phương trình là
A. \({x^2} + {y^2} + 2x + 2y - \sqrt 2 = 0\).
B. \({x^2} + {y^2} - 2x - 2y = 0\).
C. \({x^2} + {y^2} - 2x - 2y - 2 = 0\).
D. \({x^2} + {y^2} + 2x - 2y + \sqrt 2 = 0\).
Câu 29: Phương trình chính tắc của \(\left( E \right)\) có độ dài trục lớn bằng \(8\), trục nhỏ bằng \(6\) là
A. \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{36}} = 1\).
B. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{{16}} = 1\).
C. \(9{x^2} + 16{y^2} = 1\).
D. \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1\).
Câu 30: Có bao nhiêu số tự nhiên có bốn chữ số?
A. \(5040\).
B. \(4536\).
C. \(10000\).
D. \(9000\).
Câu 31: Một tổ gồm \(7\)nam và \(6\)nữ. Hỏi có bao nhiêu cách chọn \(4\) em đi trực sao cho có đúng
\(3\) nam và \(1\) nữ
A. \(204\).
B. \(1260\).
C. \(315\).
D. \(210\).
Câu 32: Số cách sắp xếp \(6\) nam sinh và \(4\) nữ sinh vào một dãy ghế hàng ngang có \(10\) chỗ ngồi là
A. \(6!.4!\).
B. \(10!\).
C. \(6! + 4!\).
D. \(6! - 4!\).
Câu 33: Một hội nghị có \(15\) nam và \(6\) nữ. Chọn ngẫu nhiên \(3\) người vào ban tổ chức. Tính xác
suất để 3 người được chọn đều là nam.
A . \(\frac{1}{2}\)
B . \(\frac{{13}}{{38}}.\)
C . \(\frac{4}{{33}}\).
D . \(\frac{1}{{11}}\).
Câu 34: Gieo hai con súc sắc cân đối, đồng chất. Xác suất để tổng số chấm xuất hiện trên hai mặt của hai con súc sắc bằng \(7\) là
A. \(\frac{6}{7}\).
B. \(\frac{1}{7}\).
C. \(\frac{1}{6}\).
D. \(\frac{5}{6}\).
Câu 35: Một tổ có \(6\) nam và \(4\) nữ. Chọn ngẫu nhiên hai người. Tính xác suất sao cho trong hai người được chọn có ít nhất một người là nữ.
A. \(\frac{4}{5}\)
B. \(\frac{2}{3}\).
C. \(\frac{2}{{15}}\).
D. \(\frac{1}{3}\).
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Trong mặt phẳng toạ độ \(Oxy\), cho đường thẳng \(\Delta :3x + 2y - 1 = 0\). Viết phương trình đường thẳng \(d\) vuông góc với đường thẳng \(\Delta \) và cách điểm \(A\left( { - 1;2} \right)\) một khoảng bằng \(\sqrt {13} .\)
Câu 37: Từ tập hợp \(E = \left\{ {0;\,1;\,2;\,3;\,4;\,5;\,6;\,7} \right\}\) có thể lập được bao nhiêu số chẵn có \(5\) chữ số đôi một khác nhau?
Câu 38: Một người kĩ sư thiết kế một đường hầm một chiều có mặt cắt là một nửa hình elip, chiều rộng của hầm là \(12m\), khoảng cách từ điểm cao nhất của elip so với mặt đường là \(3m\). Người kĩ sư này muốn đưa ra cảnh báo cho các loại xe có thể đi qua hầm. Biết rằng những loại xe tải có chiều cao \(2,8m\)thì có chiều rộng không quá \(3m\). Hỏi chiếc xe tải có chiều cao \(2,8m\)có thể đi qua hầm được không?
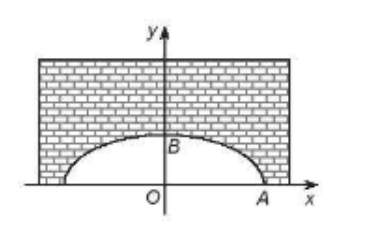
Câu 39: Cho tập \(X = \left\{ {1,2,3,4,5} \right\}.\)Gọi \(S\)là tập các số tự nhiên gồm \(6\)chữ số lấy từ \ (X.\). Chọn ngẫu nhiên một số từ \(S.\)Tính xác suất để số được chọn thỏa mãn chữ số \(1\) xuất hiện hai lần, các chữ số khác xuất hiện đúng một lần.
---------- HẾT ----------
Lời giải
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm ).

Câu 1: Tập xác định của hàm số \(y = \sqrt {x - 6} \) là
A. \(( - \infty ;6{\rm{]}}.\)
B. \([6; + \infty ).\)
C. \((6; + \infty ).\)
D. \(( - \infty ;6).\)
Phương pháp
- Căn thức xác định khi biểu thức trong căn lớn hơn bằng 0.
Lời giải
Chọn B
Điều kiện xác định: \(x - 6 \ge 0 \Leftrightarrow x \ge 6\)
Vậy tập xác định của hàm số \(y = \sqrt {x - 6} \) là \(D = [6; + \infty ).\)
Câu 2: Cho đồ thị của hàm số bậc hai như hình vẽ, trục đối xứng của đồ thị là
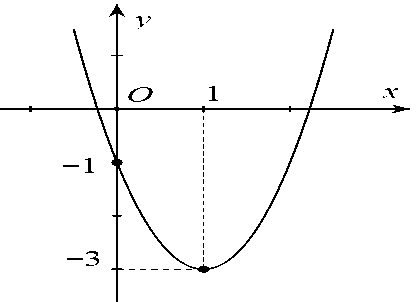
A . \(x = 1.\)
B. \(y = 1.\)
C. \(y = 0.\)
D. \(x = 0.\)
Phương pháp
Parabol\(\left( P \right):y = a{x^2} + bx + c\) \(\left( {a \ne 0} \right)\) có trục đối xứng là đường thẳng \(x = \frac{{ - b}}{{2a}}\)
Lời giải
Chọn A
Trục đối xứng của đồ thị hàm số bậc hai là đường thẳng \(x = \frac{{ - b}}{{2a}}\), với \(\frac{{ - b}}{{2a}}\) là hoành độ của đỉnh
Câu 3: Tìm khẳng định đúng trong các khẳng định sau?
A. \(f\left( x \right) = 3{x^2} + 2x - 5\)là tam thức bậc hai.
B. \(f\left( x \right) = 2x - 4\)là tam thức bậc hai.
C. \(f\left( x \right) = 3{x^3} + 2x - 1\)là tam thức bậc hai.
D. \(f\left( x \right) = {x^4} - {x^2} + 1\)là tam thức bậc hai.
Phương pháp
Tam thức bậc hai có bậc cao nhất là 2.
Lời giải
Chọn A
Theo định nghĩa tam thức bậc hai thì \(f\left( x \right) = 3{x^2} + 2x - 5\)là tam thức bậc hai.
Câu 4: Nghiệm của phương trình \(\sqrt {3x + 5} = 2\) là
A. \(x = - 1\).
B. \(x = 0\).
C. \(x = 4\).
D. \(x = - \frac{1}{3}\).
Phương pháp
Bình phương hai vế của phương trình
Lời giải
Chọn D
Bình phương hai vế của phương trình, ta được \(3x + 5 = 4\), suy ra \(x = - \frac{1}{3}\)
Thay \(x = - \frac{1}{3}\) vào phương trình đã cho ta thấy \(x = - \frac{1}{3}\) thoả mãn.
Vậy nghiệm của phương trình đã cho là \(x = - \frac{1}{3}\)
Câu 5: Cho đường thẳng \(d:x - y + 3 = 0.\) Một vectơ pháp tuyến của \(d\) là
A. \(\overrightarrow n = (1;1).\)
B. \(\overrightarrow x = (1; - 3).\)
C. \(\overrightarrow e = ( - 1; - 1).\)
D. \(\overrightarrow a = (1; - 1).\)
Phương pháp
Phương trình đường thẳng \(d:ax + by + c = 0\)có VTPT là \(\overrightarrow n = (a;b).\)
Lời giải
Chọn D
Phương trình đường thẳng \(d:x - y + 3 = 0.\)có VTPT là \(\overrightarrow a = (1; - 1).\)
Câu 6: Một vectơ chỉ phương của đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 5 - t\\y =3 + 3t\end{array}
\right.\) là
A. \(\overrightarrow x = (3;1).\)
B. \(\overrightarrow e = (5;3).\)
C. \(\overrightarrow a = (3; - 5).\)
D. \(\overrightarrow u = ( - 1;3).\)
Phương pháp
Phương trình đường thẳng \(\Delta :\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.\) có VTCP là \(\overrightarrow u = (a;b).\)
Lời giải
Chọn D
Phương trình đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 5 - t\\y = 3 + 3t\end{array} \right.\) có VTCP là \(\overrightarrow u = ( - 1;3).\)
Câu 7: Xét vị trí tương đối của hai đường thẳng \({d_1}:x - 2y + 1 = 0\) và \({d_2}: - 3x + 6y - 10 = 0\).
A. Trùng nhau.
B. Song song.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau.
Phương pháp
Sử dụng công thức vị trí tương đối của hai đường thẳng.
Lời giải
Chọn B
Câu 8: Khoảng cách từ điểm \(M\left( { - 1; - 1} \right)\) đến dường thẳng \(\Delta :4x + 3y - 18 =0\) bằng
A. \( - 5.\)
B. \(\frac{7}{5}.\)
C. \( - \frac{7}{5}.\)
D. \(5.\)
Phương pháp
Khoảng cách từ điểm \(M({x_0};{y_0})\) đến đường thẳng \(\Delta :{\rm{ }}ax + by + c = 0\) là: \(d(M,\Delta ) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
Lời giải
Chọn D
Ta có: \(d(M,\Delta ) = \frac{{\left| {4.( - 1) + 3.( - 1) - 18} \right|}}{{\sqrt {{4^2} + {3^2}} }} = 5\)
Câu 9: Phương trình nào sau đây là phương trình đường tròn?
A. \({x^2} + {y^2} - x - y + 9 = 0\).
B. \({x^2} + {y^2} - x = 0\).
C. \({x^2} + {y^2} - 2xy - 1 = 0.\)
D. \({x^2} - {y^2} - 2x + 3y - 1 = 0.\)
Phương pháp
Phương trình đường tròn có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\).
Lời giải
Chọn B
Loại C vì có số hạng \( - 2xy\).
Loại A vì: \(a = b = \frac{1}{2},\,\,c = 9 \Rightarrow {a^2} + {b^2} - c < 0\) nên không phải phương trình đường tròn.
Loại D vì trong phương trình có \( - {y^2}\).
Đáp án B có: \(a = \frac{1}{2},\,\,b = 0,\,\,c = 0 \Rightarrow {a^2} + {b^2} - c > 0\) nên là phương trình đường tròn.
Câu 10: Đường tròn \({(x - 2)^2} + {(y - 1)^2} = 4\) có bán kính là
A. \(4.\)
B. \(2.\)
C. \(16.\)
D. \(1\).
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là : \({(x - a)^2} + {(y - b)^2} = {R^2}\)
Lời giải
Chọn B
Bán kính của đường tròn là \(R = \sqrt 4 = 2\).
Câu 11: Trong mặt phẳng \(Oxy\), phương trình nào sau đây là phương trình chính tắc của một elip?
A. \(\frac{{{x^2}}}{2} + \frac{{{y^2}}}{3} = - 1\).
B. \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{8} = 1\).
C. \(\frac{x}{9} + \frac{y}{8} = 1\).
D. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{1} = 1\).
Phương pháp
Phương trình Elip \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Lời giải
Chọn D
Phương trình chính tắc của elip có dạng: \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{1} = 1\)
Câu 12: Có bao nhiêu cách chọn 1 viên bi trong chiếc hộp có 5 viên bi màu đỏ và 3 viên bi màu vàng?
A. \(8\).
B. \(15\).
C. \(6\).
D. \(4\).
Phương pháp
Áp dụng quy tắc cộng
Lời giải
Chọn A
Cách chọn 1 viên bi đỏ: có 5 cách
Cách chọn 1 viên bi vàng: có 3 cách
Theo quy tắc cộng có 5 \( + \)3 \( = \)8 cách chọn một viên bi trong hộp.
Câu 13: Có \(10\) cái bút khác nhau và \(8\)quyển sách giáo khoa khác nhau. Một bạn học sinh cần chọn \(1\) cái bút và \(1\) quyển sách. Hỏi bạn học sinh đó có bao nhiêu cách chọn?
A. \(80\).
B. \(60\).
C. \(90\).
D. \(70\).
Phương pháp
Áp dụng quy tắc nhân
Lời giải
Chọn A
Số cách chọn \(1\) cái bút có \(10\)cách, số cách chọn \(1\) quyển sách có \(8\)cách.
Vậy theo quy tắc nhân, số cách chọn \(1\) cái bút và \(1\) quyển sách là: \(10.8 = 80\)cách.
Câu 14: Có bao nhiêu cách sắp xếp \(5\) học sinh thành một hàng dọc?
A. \({5^5}\).
B.
C. \(4!\).
D. \(5\).
Phương pháp
Áp dụng công thức hoán vị
Lời giải
Chọn B
Mỗi cách sắp xếp \(5\) học sinh thành một hàng dọc là 1 hoán vị của 5 phần tử.
Vậy số cách sắp xếp \(5\) học sinh thành một hàng dọc là
Câu 15: Công thức tính số tổ hợp chập k của n phần tử là
A. \(C_n^k = \frac{{n!}}{{\left( {n - k} \right)!}}\).
B. \(C_n^k = \frac{{n!}}{{\left( {n - k} \right)!k!}}\).
C. \(A_n^k = \frac{{n!}}{{\left( {n - k} \right)!}}\).
D. \(A_n^k = \frac{{n!}}{{\left( {n - k} \right)!k!}}\).
Phương pháp
Số tổ hợp chập k của n phần tử là \(C_n^k = \frac{{n!}}{{\left( {n - k} \right)!k!}}\)
Lời giải
Chọn B
Số tổ hợp chập k của n phần tử là \(C_n^k = \frac{{n!}}{{\left( {n - k} \right)!k!}}\)
Câu 16: Số cách chọn ra \(3\)học sinh trong \(10\) học sinh bất kì là
A. \(120\)
B. \(6\).
C. \(30\).
D. \(720\).
Phương pháp
Áp dụng công thức tổ hợp
Lời giải
Chọn A
Số cách chọn ra \(3\)học sinh trong \(10\) học sinh bất kì là \(C_{10}^3 = 120\).
Câu 17: Trong khai triển nhị thức Niu-tơn của \({\left( {a + b} \right)^4}\) có bao nhiêu số hạng?
A. \(6\)
B. \(3\).
C. \(5\).
D. \(4\).
Phương pháp
Sử dụng công thức khai triển nhị thức Newton
Lời giải
Chọn C
Trong khai triển nhị thức Niu-tơn của \({\left( {a + b} \right)^4}\) có \(4 + 1 = 5\) số hạng.
Câu 18: Gieo một con xúc sắc cân đối đồng chất hai lần. Số phần tử của không gian mẫu là
A. 9.
B. 18.
C. 12.
D. 36.
Phương pháp
Sử dụng công thức đếm
Lời giải
Chọn D
Số phần tử của không gian mẫu là 6.6 \( = \)36
Câu 19: Lấy ngẫu nhiên một thẻ từ một chiếc hộp chứa \(20\) thẻ được đánh số từ \(1\) đến \(20\). Số phần tử của không gian mẫu là
A. \(n\left( \Omega \right) = 20\) .
B. \(n\left( \Omega \right) = 1\).
C. \(n\left( \Omega \right) = 10\).
D. \(n\left( \Omega \right) = 15\).
Phương pháp
Sử dụng công thức đếm
Lời giải
Chọn A
Số phần tử của không gian mẫu là \(C_{20}^1 = 20\)
Câu 20: Rút ngẫu nhiên cùng lúc ba con bài từ cỗ bài tú lơ khơ \(52\) con thì \(n\left( \Omega \right)\) bằng bao nhiêu?
A. \(140608\).
B. \(156\).
C. \(132600\).
D. \(22100\).
Phương pháp
Sử dụng công thức đếm
Lời giải
Chọn D
Ta có \(n\left( \Omega \right) = C_{52}^3 = 22100\).
Câu 21: Tập giá trị của hàm số \(y = \sqrt {x + 1} \) là
A. \(( - \infty ;0{\rm{]}}.\)
B. \([0; + \infty ).\)
C. \((1; + \infty ).\)
D. \(\left[ { - 1; + \infty } \right).\)
Phương pháp
Căn thức có tập giá trị lớn hơn bằng 0
Lời giải
Chọn D
Vì \(\sqrt {x + 1} \ge 0,\forall x \in D\) nên tập giá trị của hàm số \(y = \sqrt {x + 1} \) là \([- 1; + \infty ).\)
Câu 22: Hàm số nào sau đây có đồ thị như hình dưới đây?
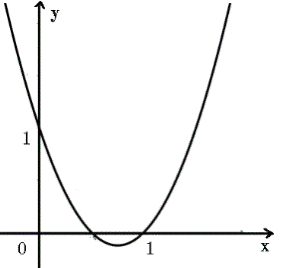
A. \(y = {x^2} - 3x + 1\).
B. \(y = - {x^2} + 3x - 1\).
C. \(y = - 2{x^2} + 3x - 1\).
D. \(y = 2{x^2} - 3x + 1\).
Phương pháp
Dựa vào dáng điệu của parabol.
Lời giải
Chọn D
Bề lõm của parabol hướng lên trên suy ra \(a > 0\), nên loại B và C
Đồ thị đi qua điểm \(\left( {1;0} \right)\)nên Chọn D
Câu 23: Cho tam thức bậc hai \(f\left( x \right) = - 2{x^2} + 8x - 8\). Trong các mệnh đề sau, mệnh đề nào đúng?
A. \(f\left( x \right) < 0\) với mọi\(x \in R\).
B. \(f\left( x \right) \ge 0\) với mọi\(x \in R\).
C. \(f\left( x \right) \le 0\) với mọi\(x \in R\).
D. \(f\left( x \right) > 0\) với mọi\(x \in R\).
Phương pháp
Sử dụng dấu của tam thức bậc hai.
Lời giải
Chọn C
Ta có \(\left\{ \begin{array}{l}\Delta = 0\\a = - 2 < 0\end{array} \right.\) suy ra \(f\left( x \right) \le 0\) với mọi\(x \in R\).
Câu 24: Phương trình \(\sqrt { - {x^2} + 4x} = 2x - 2\) có bao nhiêu nghiệm?
A. \(3\).
B. \(0\).
C. \(2\).
D. \(1\).
Phương pháp
Bình phương hai vế của phương trình
Lời giải
Chọn D
Bình phương hai vế của phương trình ta được:
\(\sqrt { - {x^2} + 4x} = 2x - 2\)\( \Rightarrow - {x^2} + 4x = {\left( {2x - 2} \right)^2}\)\( \Leftrightarrow 5{x^2} - 12x + 4 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = \frac{2}{5}\end{array} \right.\).
Với hai giá trị tìm được, chỉ có \(x = 2\)thỏa mãn phương trình đã cho
Vậy \(x = 2\) là nghiệm của phương trình. Do đó phương trình đã cho có 1 nghiệm
Câu 25: Phương trình tham số của đường thẳng qua \(M\left( {1; - 1} \right)\), \(N\left( {4;3} \right)\) là
A. \(\left\{ \begin{array}{l}x = 3 + t\\y = 4 - t\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x = 1 + 3t\\y = 1 + 4t\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x = 3 - 3t\\y = 4 - 3t\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x = 1 + 3t\\y = - 1 + 4t\end{array} \right.\).
Phương pháp
Phương trình tham số của đường thẳng qua \(M\left( {{x_0};{y_0}} \right)\), có một véctơ chỉ phương \(\overrightarrow u = \left( {a;\;b} \right)\) là \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.\)
Lời giải
Chọn D
Đường thẳng đi qua hai điểm \(M\left( {1; - 1} \right)\), \(N\left( {4;3} \right)\) có một véctơ chỉ phương \(\overrightarrow {MN} = \left( {3;\;4} \right)\).
Phương trình tham số của đường thẳng qua \(M\left( {1; - 1} \right)\), \(N\left( {4;3} \right)\) là \(\left\{ \begin{array}{l}x = 1 + 3t\\y = - 1 + 4t\end{array} \right.\).
Câu 26: Góc giữa hai đường thẳng \(a:\,\sqrt 3 x - y + 7 = 0\) và \(b:x - \sqrt 3 y - 1 = 0\) là
A. \(30^\circ \).
B. \(90^\circ \).
C. \(60^\circ \).
D. \(45^\circ \).
Phương pháp
Áp dụng công thức tính góc giữa hai đường thẳng có: \(\cos \left( {a,b} \right) = \frac{{\overrightarrow {{n_1}} .\overrightarrow {{n_2}} }}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}}\).
Lời giải
Chọn A
Đường thẳng \(a\) có vectơ pháp tuyến là: \(\overrightarrow {{n_1}} = \left( {\sqrt 3 ;\, - 1} \right)\);
Đường thẳng \(b\) có vectơ pháp tuyến là: \(\overrightarrow {{n_2}} = \left( {1;\, - \sqrt 3 } \right)\).
Áp dụng công thức tính góc giữa hai đường thẳng ta có:
\(\cos \left( {a,b} \right) = \left| {\cos (\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} )} \right| = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {1.\sqrt 3 + \left( { - 1} \right)\left( { - \sqrt 3 } \right)} \right|}}{{2.2}} = \frac{{\sqrt 3 }}{2}\).
Suy ra góc giữa hai đường thẳng bằng \(30^\circ \).
Câu 27: Đường tròn tâm \(I( - 1;2)\) và đi qua điểm \(M(2;1)\) có phương trình là
A. \({x^2} + {y^2} + 2x - 4y - 5 = 0\).
B. \({x^2} + {y^2} + 2x - 4y - 3 = 0.\)
C. \({x^2} + {y^2} - 2x - 4y - 5 = 0\).
D. \({x^2} + {y^2} + 2x + 4y - 5 = 0.\)
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là : \({(x - a)^2} + {(y - b)^2} = {R^2}\)
Lời giải
Chọn A
Đường tròn có tâm \(I\left( { - 1;2} \right)\) và đi qua \(M\left( {2;1} \right)\) thì có bán kính là: \(R = IM = \sqrt {{3^2} + {{\left( { - 1} \right)}^2}} = \sqrt {10} \)
Khi đó có phương trình là: \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 10 \Leftrightarrow {x^2} + {y^2} + 2x - 4y - 5 = 0\)
Câu 28: Đường tròn đi qua 3 điểm \(A\left( {0;2} \right),{\rm{ }}B\left( {2;2} \right),{\rm{ }}C(1;1 + \sqrt 2)\)có phương trình là
A. \({x^2} + {y^2} + 2x + 2y - \sqrt 2 = 0\).
B. \({x^2} + {y^2} - 2x - 2y = 0\).
C. \({x^2} + {y^2} - 2x - 2y - 2 = 0\).
D. \({x^2} + {y^2} + 2x - 2y + \sqrt 2 = 0\).
Phương pháp
Phương trình đường tròn có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\,\,\left( {{a^2} + {b^2} - c > 0} \right)\).
Lời giải
Chọn B
Gọi phương trình đường tròn cần tìm có dạng: \({x^2} + {y^2} - 2ax - 2by + c = 0\,\,\left( {{a^2} + {b^2} - c > 0} \right)\).
Đường tròn đi qua 3 điểm \(A\left( {0;2} \right),{\rm{ }}B\left( {2;2} \right),{\rm{ }}C(1;1 + \sqrt 2 )\)nên ta có:
\(\left\{ \begin{array}{l}4 - 4b + c = 0\\8 - 4a - 4b + c = 0\\4 + 2\sqrt 2 - 2a - 2\left( {1 + \sqrt 2 } \right)b + c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 1\\c = 0\end{array} \right.\)
Vậy phương trình đường tròn đi qua 3 điểm \(A\left( {0;2} \right),{\rm{ }}B\left( {2;2} \right),{\rm{ }}C(1;1 + \sqrt 2 )\) là:
\({x^2} + {y^2} - 2x - 2y = 0\)
Câu 29: Phương trình chính tắc của \(\left( E \right)\) có độ dài trục lớn bằng \(8\), trục nhỏ bằng \(6\) là
A. \(\frac{{{x^2}}}{64} + \frac{{{y^2}}}{36} = 1\).
B. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{16} = 1\).
C. \(9{x^2} + 16{y^2} = 1\).
D. \(\frac{{{x^2}}}{16} + \frac{{{y^2}}}{9} = 1\).
Phương pháp
Phương trình Elip \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Lời giải
Chọn D
Ta có: \(\left\{ \begin{array}{l}2a = 8\\2b = 6\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}a = 4\\b = 3\end{array} \right.\).
Vậy phương trình chính tắc của \(\left( E \right)\): \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1\)
Câu 30: Có bao nhiêu số tự nhiên có bốn chữ số?
A. \(5040\).
B. \(4536\).
C. \(10000\).
D. \(9000\).
Phương pháp
Sử dụng quy tắc cộng và quy tắc nhân.
Lời giải
Chọn D
Gọi số tự nhiên cần tìm là \(n = \overline {abcd} \), trong đó \(a,\,b,\,c,\,d \in \left\{ {0,1,2,3,4,5,6,7,8,9} \right\}\) và \(a \ne 0\).
Ta có: \(a\) có \(9\) cách chọn; \(b,c,d\) mỗi số có \(10\) cách chọn.
Vậy có: \({9.10^3} = 9000\) số cần tìm.
Câu 31: Một tổ gồm 7 nam và 6 nữ. Hỏi có bao nhiêu cách chọn 4 em đi trực sao cho có đúng 3 nam và 1 nữ
A. \(204\).
B. \(1260\).
C. \(315\).
D. \(210\).
Phương pháp
Áp dụng công thức tổ hợp
Lời giải
Chọn D
Chọn 4 em đi trực sao cho có đúng 3 nam và 1 nữ:
+ Chọn 3 nam có \(C_7^3\)cách.
+ Chọn 1 nữ có \(C_6^1\)cách
Vậy có \(C_7^3\).\(C_6^1 = 210\) cách.
Câu 32: Số cách sắp xếp \(6\) nam sinh và \(4\) nữ sinh vào một dãy ghế hàng ngang có \(10\) chỗ ngồi là
A. \(6!.4!\).
B. \(10!\).
C. \(6! + 4!\).
D. \(6! - 4!\).
Phương pháp
Áp dụng công thức chỉnh hợp
Lời giải
Chọn B
Có \(10\) học sinh xếp vào một dãy ngế hàng ngang có \(10\) chỗ ngồi nên có \(10!\) cách.
Câu 33: Một hội nghị có 15 nam và 6 nữ. Chọn ngẫu nhiên 3 người vào ban tổ chức. Tính xác suất để 3 người được chọn đều là nam.
A . \(\frac{1}{2}\).
B . \(\frac{{13}}{{38}}.\)
C . \(\frac{4}{{33}}\).
D . \(\frac{1}{{11}}\).
Phương pháp
Áp dụng công thức tính xác suất
Lời giải
Chọn B
\(n\left( \Omega \right) = C_{21}^3 = 1330\).
Gọi A là biến cố: “3 người được chọn đều là nam”. Khi đó, \(n\left( A \right) = C_{15}^3 = 455\).
Vậy xác suất để 3 người được chọn đều là nam: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{13}}{{38}}.\)
Câu 34: Gieo hai con súc sắc cân đối, đồng chất. Xác suất để tổng số chấm xuất hiện trên hai mặt của hai con súc sắc bằng \(7\) là
A. \(\frac{6}{7}\).
B. \(\frac{1}{7}\).
C. \(\frac{1}{6}\).
D. \(\frac{5}{6}\).
Phương pháp
Áp dụng công thức tính xác suất
Lời giải
Chọn C
Số phần tử của không gian mẫu là \(n\left( \Omega \right) = 6 \times 6 = 36\).
Gọi \(A\) là biến cố “Tổng số chấm xuất hiện trên hai mặt của hai con súc sắc bằng \(7\)”. Ta có
\(A = \left\{ {\left( {1;6} \right),\left( {2;5} \right),\left( {3;4} \right),\left( {4;3} \right),\left( {5;2} \right),\left( {6;1} \right)} \right\}\)\( \Rightarrow n\left( A \right) = 6\).
Vậy \(P\left( A \right) = \frac{6}{{36}} = \frac{1}{6}\).
Câu 35: Một tổ có \(6\) nam và \(4\) nữ. Chọn ngẫu nhiên hai người. Tính xác suất sao cho trong hai người được chọn có ít nhất một người là nữ.
A. \(\frac{4}{5}\).
B. \(\frac{2}{3}\).
C. \(\frac{2}{{15}}\).
D. \(\frac{1}{3}\).
Phương pháp
Áp dụng công thức tính xác suất
Lời giải
Chọn B
Số phần tử không gian mẫu là số cách chọn \(2\) người trong \(10\) người: \(n\left( \Omega \right) = C_{10}^2\).
Gọi \(A\) là biến cố hai người được chọn có ít nhất một người là nữ.
Suy ra \(\bar A\) là biến cố cả hai người là nam.
Ta có : \(n\left( {\bar A} \right) = C_6^2\).
Do đó xác suất \(P\left( A \right) = 1 - \frac{{C_6^2}}{{C_{10}^2}} = \frac{2}{3}\).
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Trong mặt phẳng toạ độ \(Oxy\), cho đường thẳng \(\Delta :3x + 2y - 1 = 0\). Viết phương trình đường thẳng \(d\) vuông góc với đường thẳng \(\Delta \) và cách điểm \(A\left( { - 1;2} \right)\) một khoảng bằng \(\sqrt {13} .\)
Phương pháp
Khoảng cách từ điểm \(M({x_0};{y_0})\) đến đường thẳng \(\Delta :{\rm{ }}ax + by + c = 0\) là: \(d(M,\Delta ) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
Lời giải
Do \(d \bot \Delta \Rightarrow \overrightarrow {{n_d}} = \left( { - 2;3} \right)\)
Nên phương trình đường thẳng \(d\)có dạng: \( - 2x + 3y + c = 0\)
Ta có: \(d(A,d) = \frac{{\left| { - 2.( - 1) + 3.2 + c} \right|}}{{\sqrt {{{( - 2)}^2} + {3^2}} }} = \sqrt {13} \)
Giải phương trình ta được \(c = 5\) hoặc \(c = - 21\).
Vậy phương trình đường thẳng \(d\) là: \( - 2x + 3y + 5 = 0\) hoặc \( - 2x + 3y - 21 = 0\).
Câu 37: Từ tập hợp \(E = \left\{ {0;\,1;\,2;\,3;\,4;\,5;\,6;\,7} \right\}\) có thể lập được bao nhiêu số chẵn có \(5\) chữ số đôi một khác nhau?
Phương pháp
Sử dụng quy tắc đếm
Lời giải
Gọi số cần tìm là \(\overline {abcde} \)
Trường hợp 1:
Chọn \(e = 0\) có 1 cách
Chọn \(a;\,b;\,c;\,d\)ta chọn \(4\) phần tử trong 7 phần tử và sắp thứ tự có \(A_7^4\)cách chọn.
Vậy có \(1.A_7^4 = 840\)số.
Trường hợp 2:
Chọn \(e \ne 0\) mà \(e\) là số chẵn có 3 cách
Chọn \(a\) có 6 cách.
Chọn \(\,b;\,c;\,d\) ta chọn 3 phần tử trong 6 phần tử và sắp thứ tự có \(A_6^3\) cách chọn.
Vậy có \(3.6.A_6^3 = 2160\)số.
\( \Rightarrow \) có \(840 + 2160 = 3000\) số có \(5\) chữ số khác nhau đôi một lấy từ \(E\) là số chẵn.
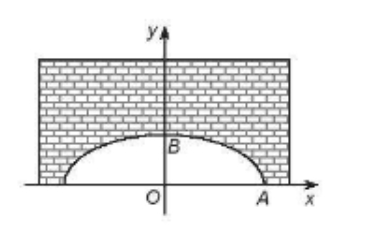
Câu 38: Một người kĩ sư thiết kế một đường hầm một chiều có mặt cắt là một nửa hình elip, chiều rộng của hầm là 12m, khoảng cách từ điểm cao nhất của elip so với mặt đường là 3m. Người kĩ sư này muốn đưa ra cảnh báo cho các loại xe có thể đi qua hầm. Biết rằng những loại xe tải có chiều cao 2,8m thì có chiều rộng không quá 3m. Hỏi chiếc xe tải có chiều cao 2,8m có thể đi qua hầm được không?
Phương pháp
Phương trình chính tắc của (E) là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\,\), trong đó \(a > b > 0\)
Lời giải
Phương trình chính tắc của (E) là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\,\), trong đó \(a > b > 0\)
Do các điểm \(B(0;3)\) và \(A(6;0)\) thuộc (E) nên thay vào phương trình của (E) ta có \(b = 3\)và \(a = 6\), suy ra phương trình của (E) là: \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{9} = 1\,\)
Với những xe tải có chiều cao 2,8m, chiều rộng của xe tải là 3m, tương ứng với \(x = 1,5\). Thay vào phương trình của elip để tìm ra độ cao y của điểm M (có hoành độ bằng 1,5 thuộc (E)) so với trực Ox.
\({y_M} = 3.\sqrt {1 - \frac{{x_M^2}}{{16}}} = 3.\sqrt {1 - \frac{{{{1,5}^2}}}{{16}}} \approx 2,905 > 2,8.\)
Vậy Ô tô tải có thể đi được qua hầm, tuy nhiên cần khuyến cáo ô tô phải đi vào chính giữa hầm.
Câu 39: Cho tập \(X = \left\{ {1,2,3,4,5} \right\}.\)Gọi \(S\)là tập các số tự nhiên gồm \(6\)chữ số lấy từ \(X.\)Chọn ngẫu nhiên một số từ \(S.\)Tính xác suất để số được chọn thỏa mãn chữ số \(1\) xuất hiện hai lần, các chữ số khác xuất hiện đúng một lần.
Phương pháp
Sử dụng quy tắc đếm
Lời giải
Số các số tự nhiên gồm \(6\)chữ số lấy từ \(X\)là: 5.5.5.5.5.5=15625
Số phần tử không gian mẫu:\(n(\Omega ) = C_{15625}^1\, = 15625\,\)
Gọi A là biến cố: “Số được chọn thỏa mãn chữ số \(1\) xuất hiện hai lần, các chữ số khác xuất hiện đúng một lần.”
\( \Rightarrow n(A) = C_6^2.4! = 360 \Rightarrow P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{360}}{{15625}} = \frac{{72}}{{3125}}.\)
---------- HẾT ---------